Modeling and data analysis of rainfall in the tropics
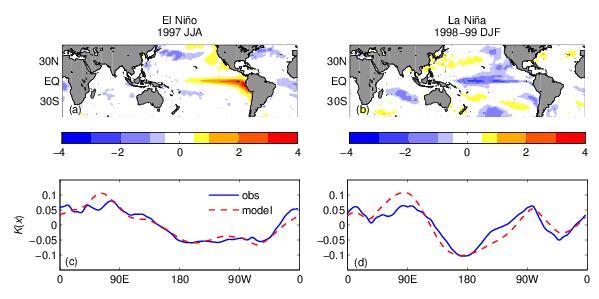
Rainfall and clouds, i.e. convection, in the tropics occurs on many temporal and spatial scales. Increasing our understanding of tropical convection is essential due both to its large economic and societal impacts in the tropics as well as its close connections to events in the midlatitudes and beyond. My primary contributions to this field have thus far been in the development and use of methods for both model assessment and data analysis of large datasets. These methods are based on mathematical theories for large-scale phenomena in the tropical atmosphere and have been applied to models of the Walker circulation, the Madden-Julian oscillation (MJO) and convectively-coupled equatorial waves (CCEWs).
Majda, A.J., Stechmann, S.N., Chen, S., Ogrosky, H.R. & Thual, S. 2019 Explaining Tropical Intraseasonal Variability with the Stochastic Skeleton Model. Springer Briefs in Mathematics of Planet Earth. 123 pages.
Ogrosky, H.R., Stechmann, S.N. & Hottovy, S. 2019 Instability and nonlinear dynamics of the MJO in a tropical channel model with vertically-varying convective adjustment. Theor. Comp. Fluid Dyn. 33, 307-323.
Ogrosky, H.R., Stechmann, S.N., Chen, N. & Majda, A.J. 2019 Singular Spectrum Analysis with conditional predictions for real-time state estimation and forecasting. Geophys. Res. Lett. 46, 1851-1860.
Ogrosky, H.R., Stechmann, S.N. & Majda, A.J. 2017 Boreal summer intraseasonal oscillations in the MJO skeleton model with observation-based forcing. Dyn. Atmos. Oceans 78, 38-56.
Ogrosky, H.R. & Stechmann, S.N. 2016 Identifying convectively coupled equatorial waves using theoretical wave eigenvectors. Mon. Wea. Rev. 144, 2235-2264.
Ogrosky, H.R. & Stechmann, S.N. 2015 Assessing the equatorial long-wave approximation: asymptotics and observational data analysis. J. Atmos. Sci. 72, 4821-4843.
Ogrosky, H.R. & Stechmann, S.N. 2015 The MJO skeleton model with an observation-based background state and forcing. Quart. J. Roy. Meteor. Soc. 141, 2654-2669.
Stechmann, S.N. & Ogrosky, H.R. 2014 The Walker circulation, diabatic heating, and outgoing longwave radiation. Geophys. Res. Lett. 41, 9097-9105.
Selected as "AGU Research Spotlight": Minnehan, C. 2015 Rethinking how tropical convection works, Eos 96, doi: 10.1029/2015EO032677.
Modeling film flows in cylindrical geometries
 |
|
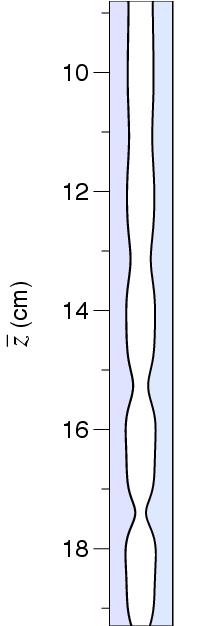
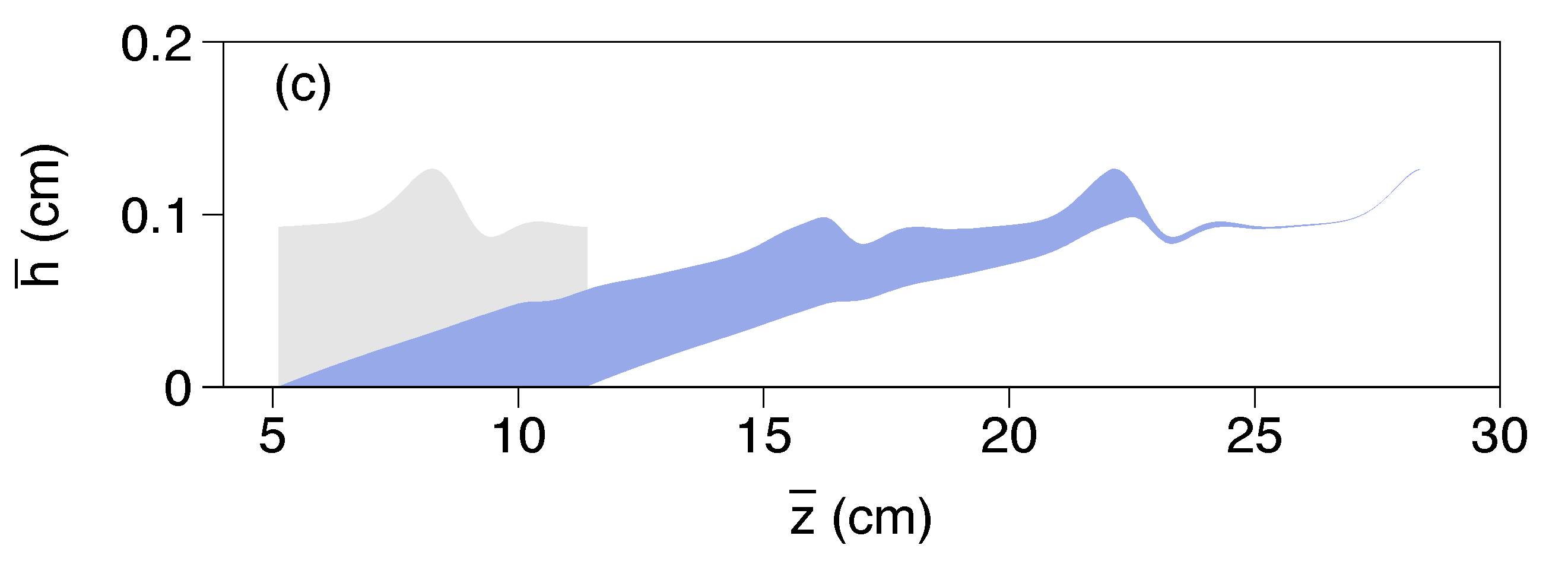
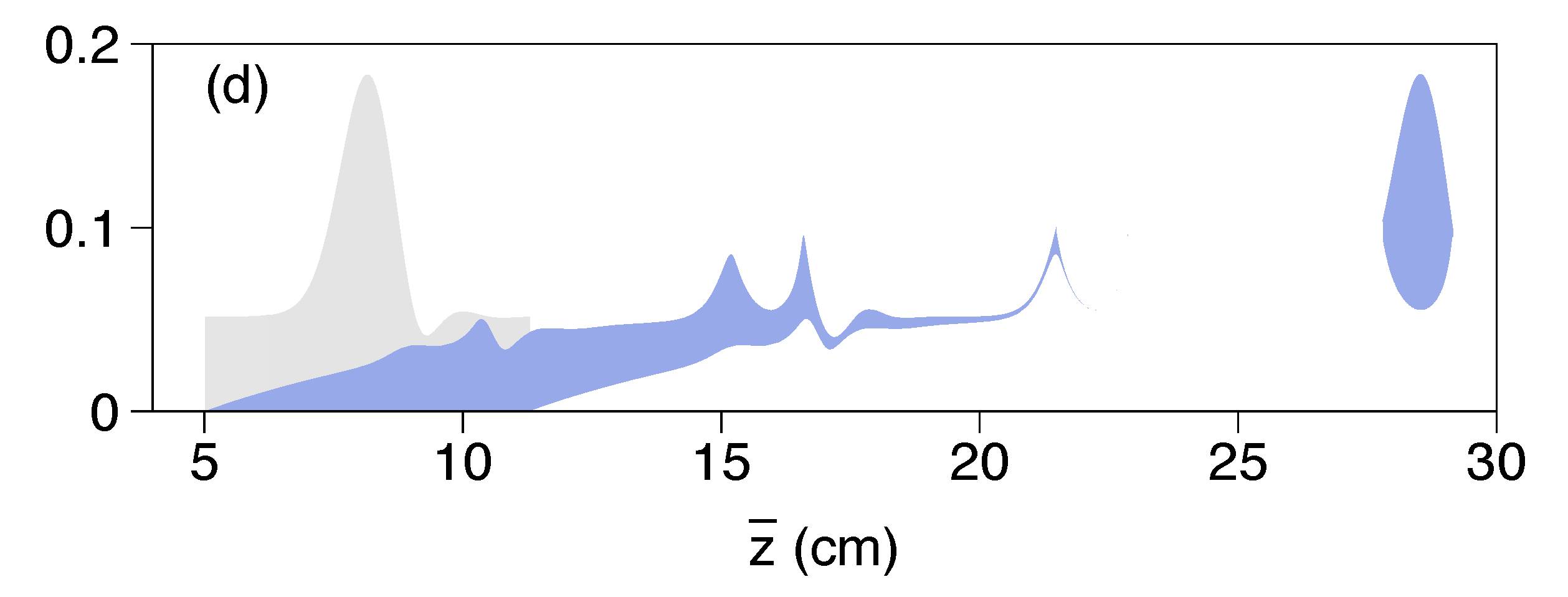
The flow of thin films is an important area of research due to the wide variety of applications across the sciences and engineering. My work has been motivated by biological applications. Human airways are lined with a thin layer of mucus, which traps harmful particles and transports them away from the lungs. For patients with diseases like cystic fibrosis whose cilia do not function properly, an important mechanism for this transport can be airflow during breathing or coughing. With this as motivation, I have studied simplified setups of this problem, namely the flow of a viscous fluid film lining the interior of a vertical tube. Such flows are unstable to long-wave perturbations. My primary contributions to this field have been the development and study of a series of models describing the growth and saturation of these instabilities.
Camassa, R., Ogrosky, H.R. & Olander, J. submitted. Low-Reynolds small amplitude flow of an Upper Convected Maxwell liquid in a vertical tube.
Ogrosky, H.R. submitted. On the impact of viscosity ratio on falling two-layer viscous film flow inside a tube.
Ogrosky, H.R. 2021 Linear stability and nonlinear dynamics in a long-wave modell of film flows inside a tube in the presence of surfactant. J. Fluid Mech. 908, A23-1-35.
Camassa, R., Marzuola, J., Ogrosky, H.R. & Swygert, S. 2021 On the stability of traveling wave solutions to thin-film and long-wave models for film flows inside a tube. Physica D 415, 132750-1-9.
Camassa, R., Ogrosky, H.R. & Olander, J. 2017 Viscous film flow coating the interior of a vertical tube. Part 2. Air-driven flow. J. Fluid Mech. 825, 1056-1090.
Camassa, R., Marzuola, J., Ogrosky, H.R. & Vaughn, N. 2016 Traveling waves for a model of gravity-driven film flows in cylindrical domains. Physica D 333, 254-265.
Camassa, R. & Ogrosky, H.R. 2015 On viscous film flows coating the interior of a tube: thin-film and long-wave models. J. Fluid Mech. 772, 569-599.
Camassa, R., Ogrosky, H.R. & Olander, J. 2014 Viscous film flow coating the interior of a vertical tube. Part I. Gravity-driven flow. J. Fluid Mech. 745, 682-715.
Camassa, R., Forest, M.G., Lee, L., Ogrosky, H.R. & Olander, J. 2012 Ring waves as a mass transport mechanism in air-driven core-annular flows. Phys. Rev. E 86, 066305-1-11.
Ogrosky, H.R., Modeling Liquid Film Flow Inside a Vertical Tube, Ph.D. Thesis, University of North Carolina, 2013.