Graph Theory
Math 330 |
Spring 2004
B -Track
Copley 244
|
| Instructor: Richard Hammack |
Office hours: |
| Office: 238 Copley |
Monday, 2:45--3:45 |
| Work: 752-7210 (and voice mail) |
Tuesday, 10:00 -- 11:30 |
| Home: 353-8572 (before 9:30 p.m., please) |
Wednesday,12:00--1:30 |
| Fax: 752-4724 |
Friday, 8:30--9:30 |
| E-mail: rhammack@rmc.edu |
and by appointment |
Prerequisite: Mathematics 220 or permisson of the instructor
Text: Graphs and Digraphs, by Gary Chartrand and Linda Lesniak,
Third edition
Graph theory is a relatively new branch of mathematics. Although it was created
to solve recreational problems involving games, it has in the past 60 years
become a mature mathematical theory with important applications to computer
science, operations research, chemistry, electrical networks and signal processing,
among many other disciplines.
|
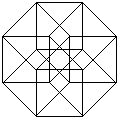
Simply put, a graph is a set of points with lines connecting them. The
figure here is an example of a typical graph. Graph theory is concerned
with the properties of such figures.
Results in graph theory can be very easy to understand but notoriously
difficult to prove. You may have heard of the famous "Four color
thoerem." This theorem states that only four colors are needed to
color any map so that no two countries sharing a common border have the
same color. This problem was posed in 1852 by a British college student
who observed that he never needed more than four colors for a map. His
professors were unable to verify or refute the statement, and the problem
became well known in mathematical circles. Despite efforts by some of
the best mathematicians in the world, this problem remained unsolved for
nearly 125 years. It was finally solved in 1976, and the proof was hundreds
of pages long. The event was a major milestone in the history of mathematics.
|
 |
Not all graph theory problems are this difficult. Many unsolved problems probably
have relatively simple solutions that require only a clever insight. Other questions
about graph theory have not even been asked yet. If you have a taste for
this subject, the work you do in this class can prepare you to do original research
in a SURF or independent study project.
Course topics include degree sequences, trees, Eulerian and Hamiltonian graphs,
matching, factoring, coloring, planar graphs, connectivity, Menger's Theorem
and networks. You are expected to prove theorems and understand applications
of the material to practical problems.
Material from Chapters 1 - 6 and 8 - 9 is covered. Weekly reading assignments
from these chapters are given. You should read the material before we discuss
it in class, and again after we discuss it. Your grade is determined by homework
assignments, a midterm, and a final exam. Details follow.
Homework: I will not assign any homework problems. Instead, you will
work those exercises in the text that you find most interesting, subject to
the following guidelines. I have divided all the exercises into two groups,
A and B, as indicated on the Homework List
attached to this syllabus. Group A consists mostly of problems that require
proofs, while Group B consists mostly of routine or computational problems.
For each section of the text we cover, you are required to do at least two exercises,
at least one of which must be from Group A.
- You can turn the problems in at any time you wish, though it is wise to
do at least 5 problems per week.
- If a solution or proof is wrong, I will return it to you and you can submit
a revised version.
- Exceptionally messy or illegible work is not graded.
- I am attentive to how well you communicate your ideas. I may ask you to
redo a correct proof that is badly worded or awkwardly organized.
- I encourage you to work together on homework, though the work you turn
in must be your own.
- Some homework problems are intended to make you think about ideas not discussed
in class.
Midterm: There will be one closed-book midterm test. The date will be
decided upon later. A makeup test will be given in the event of an excused absence.
An unexcused absence from the test results in a grade of zero.
Final Exam: The final exam is comprehensive, and is scheduled for Wednesday,
May 19, 8:30--11:30. A makeup final exam can only be given with consent of the
Dean's office.
Optional Project: Instead of taking the final exam, you have the option
of doing a project. This project should be a paper on a graph theory topic of
your choice, subject to my approval. If you wish to take this option, please
consult with me before spring break. Doing a project may not be easier than
taking the final exam, but it will most likely be (even) more interesting.
Grading: Suppose that by the last day of class you have worked (correctly)
x problems from Group A and y problems from Group B, subject to
the guidelines explained above. Your grade will be determined as follows.
| Requiremtents for a grade of "A" |
1. The inequality 2x +y > 100 holds
2. Satisfactory grade on midterm ("A" or "B")
3. Satisfactory grade on final exam ("A" or "B") |
| Requiremtents for a grade of "B" |
1. The inequality 2x +y > 75 holds
2. Satisfactory grade on midterm ("A" or "B")
3. Satisfactory grade on final exam ("A" or "B") |
| Requiremtents for a grade of "C" |
Exactlly one of the requirements for a "B" is not met |
| Requiremtents for a grade of "D" |
Exactlly two of the requirements for a "B" are not met |
| Requiremtents for a grade of "F" |
Exactlly three of the requirements for a "B" are not
met |
Attendance: I do not take attendance, but I do notice if you are not
attending class. If your grades are high, I do not mind if you miss class. However,
if your grades are low and you miss a lot of class, I will notify your advisor
and the Dean of Students. As a matter of courtesy, you should arrive punctually
and stay for the entire duration of each class you attend. Please inform me
ahead of time if you must leave early.
Cell Phones: Please be sure that all cell phones and pagers are turned
off for the entire duration of each class.
Internet: Information about this course is posted on the Internet. To
find it, go to my home page (http://faculty.rmc.edu/rhammack/) and
click on "Math 330." There you will find the syllabus, homework assignments,
a calendar, and other announcements.
Office: Please feel free to stop by my office whenever you have a question,
or if you just want to chat. If my posted hours are inconvenient, I will be
happy to schedule an appointment.
Tell me if you are having trouble. Catching up can be very difficult once
you get behind, so let me know as soon as you think there is a problem.
Notice: The Americans with Disabilities Act of 1990 and other Federal
laws require Randolph-Macon College to provide a "reasonable accommodation"
to any individual who advises us of a physical, psychological, or learning disability.
If you have a physical, psychological, or learning disability that requires
an accommodation, you must first register with the Office for Disability Support
Services, located in the Higgins Academic Center.
