_______________________________________________________________________
Calculus  II                                                 Test #2                                      March 18, 2005

Name____________________           R.  Hammack                                     Score ______
______________________________________________________________________

(1) Find the area of the region contained between the graphs of y=x^2+1  and y=x,  and between x=-1 and x=2.

  ∫_ (-1)^2 (x^2 + 1 - x) dx =[x^3/3 + x - x^2/2] _ (-1)^2 = (2^3/3 + 2 - 2^2/2) - ((-1)^3/3 + (-1) - (-1)^2/2)  = 8/3 + 2 - 2 + 1/3 + 1 + 1/2 = 9/2Square units [Graphics:HTMLFiles/T2S05D_3.gif]

 

(2) Find the area of the region contained between the curves  y =x^2/2 and  y =1/(1 + x^2).

These curves intersect at points with x coordinates that satisfy x^2/2=1/(1 + x^2) [Graphics:HTMLFiles/T2S05D_10.gif]
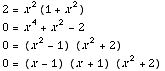
2 = x^2(1 + x^2)  0 = x^4 + x^2 - 2  0 = (x^2 - 1) (x^2 + 2)  0 = (x - 1) (x + 1) (x^2 + 2)
Thus, the curves intersect at x = 1 and  x = -1.

∫_ (-1)^1 (1/(1 + x^2) - x^2/2) dx =[tan^(-1) (x) - x^3/6] _ (-1)^1 = (tan^(-1) (1) - ... an^(-1) (-1) - (-1)^3/6)  = π/4 - 1/6 + π/4 - 1/6 = π/2 - 1/3Square units

 

(3) Consider the region contained between the graphs of y=cos(x)^(1/2),  y=0, x=0, and x=π/3,
This region is revolved around the x-axis. Find the volume of the resulting solid.

By slicing:
∫_0^(π/3) πcos(x)^(1/2)^2dx = π∫_0^(π/3) cos(x) dx = π[ sin(x) ] _0^(π/3)  = π ( sin(π/3) - sin(0)) = (π3^(1/2))/2Cubic Units . [Graphics:HTMLFiles/T2S05D_13.gif]

 

(4) Consider the region contained between the graphs of y=x^3-2x^2+x  and  y=0.
This region is revolved around the y-axis. Find the volume of the resulting solid.

Note  y = x^3-2x^2+x = x(x^2-2x+1) = x(x - 1)^2, so the x intercepts are 0 and 1.
Drawing a rough sketch of the graph, we see that the region lies between 0 and 1 on the x-axis[Graphics:HTMLFiles/T2S05D_20.gif]

 

Volume by shells:
∫_0^12π x(x^3-2x^2+x)dx = 2π∫_0^1(x^4-2x^3+x^2)dx = 2π[ x^5/5 - x^4/2 + x^3/3 ] _0^1 = 2π( 1/5-1/2+1/3) = 2π( 6/30-15/30+10/30) = π/15 Cubic Units

(5) Find the exact arc length of the curve  y = f(x) = ∫_1^x(2t + t^2)^(1/2)dt  between x=1 and x=2.

Note: f'(x)=(2x + x^2)^(1/2).  Now using the arc length formula, we get
 ∫_1^2(1 + (f ' (x))^2)^(1/2)dx = ∫_1^2(1 + ((2x + x^2)^(1/2))^2)^(1/2)dx = ∫_1^2(1 + 2x + x^2)^(1/2)dx = ∫_1^2(1 + x)^2^(1/2)dx=∫_1^2(1+x)dx = [ x + x^2/2] _1^2 = (2+2^2/2)-(1+1^2/2) = 2+2-1-1/2 = 5/2  Units.




(6) Consider the graph of y=x/2+1 between x=1 and x=3.  This graph is revolved around the x-axis. Find the area of the resulting surface.
Using the arc length formula, we get
 ∫_1^32π(x/2+1)(1 + (1/2)^2)^(1/2)dx = 2π∫_1^3(x/2+1)(5/4)^(1/2)dx = π5^(1/2)∫_1^3(x/2+1)dx = π5^(1/2)[ x^2/4 + x] _1^3 = π5^(1/2)((3^2/4+3)-(1^2/4+1)) = π5^(1/2)(9/4+3-1/4-1) = 4π5^(1/2)   Square Units.

(7) A variable force pushes an object 10 feet along a straight line in such a way that when the object is x feet from its starting point, the force on the object is  2-11/(x + 1)^2 pounds. How much work is done in moving the object 10 feet?

Work =∫_0^10 ( 2-11/(x + 1)^2)dx = [ 2x + 11/(x + 1) ] _0^10 = (20+11/(10 + 1))-(0+11/(0 + 1)) = 10 Foot pounds