___________________________________________________________
Calculus  II                                           Quiz #7                     April 22, 2005

Name_________________            R.  Hammack                  Score ______
___________________________________________________________
(1) Decide if the following sequences converge or diverge. In the case of convergence, state the limit if it can be determined.

(a)    -1 RowBox[{RowBox[{RowBox[{{, , Cell[TextData[Cell[BoxData[tan (n)]]], FontSize -> 12], , }}], _, (n = 1)}], ^, ∞}]

Underscript[lim , n∞]tan^(-1)(n) =π/2  (SEQUENCE CONVERGES)


(b)    -1 RowBox[{RowBo ... n, Cell[TextData[Cell[BoxData[tan (n)]]], FontSize -> 12]}], , }}], _, (n = 1)}], ^, ∞}]

Odd terms approach -π/2, even terms approach π/2. THUS THE SEQUENCE DIVERGES


(c)  (1/1-1/2),(1/2-1/3),(1/3-1/4),(1/4-1/5),(1/5-1/6),...

The nth term is 1/n-1/(n + 1)=1/n(n + 1).
Underscript[lim , n∞]1/n(n + 1)= 0 (SEQUENCE CONVERGES)


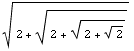(d)    2^(1/2), (2 + 2^(1/2))^(1/2), (2 + (2 + 2^(1/2))^(1/2))^(1/2), (2 + (2 + (2 + 2^(1/2))^(1/2))^(1/2))^(1/2), ...

Note: The series is defined recursively as a_1=2^(1/2)and  a_ (n + 1)=(2 + a_n)^(1/2).
If the sequence has a limit L, then L = Underscript[lim , n∞]a_ (n + 1)=Underscript[lim , n∞](2 + a_n)^(1/2)
which gives L = (2 + L)^(1/2), or L^2 = 2+L.
Thus
L^2- L - 2 = 0
(L - 2)(L + 1) = 0
So L is either 2 or -1.
But the series has positive terms, so it couldn't converge to a negative number.
Thus, if it converges, it must converge to 2.

But does it converge?
From its definition, it should be clear that the sequence is increasing.
Also, notice that it has 2 is an upper bound, for:
a_1=2^(1/2)< 2
a_2=(2 + a_1)^(1/2)<(2 + 2)^(1/2)= 2
a_3=(2 + a_2)^(1/2)<(2 + 2)^(1/2)= 2
a_4=(2 + a_3)^(1/2)<(2 + 2)^(1/2)= 2, and so on.
Thus, it is an increasing sequence that is bounded above.
Therefore must converge, and as computed above, it converges to 2.