_______________________________________________________________________
Calculus  II                                                 Test #2                                      March 19, 2004

Name____________________           R.  Hammack                                     Score ______
______________________________________________________________________

(1) Find the area of the region contained between the graphs of y = e^x,  y = e^(2x), and x = ln(3).
Simplify your final answer as much as possible.

[Graphics:HTMLFiles/test2_4.gif]

∫_0^ln (3) (e^(2x) - e^x) dx =[e^(2x)/2 - e^x] _0^ln(3) = (e^(2ln(3))/2 - e^ln(3)) - (e^0/2 - e^0) =
(e^ln(3^2)/2 - 3) - (1/2 - 1) = 9/2 - 3 - 1/2 + 1 = 2 square units


(2) Consider the region contained between the curves y = x^2 and  y = x^(1/2).
This region is revolved around the x-axis. What is the volume of the resulting solid?

[Graphics:HTMLFiles/test2_9.gif]

Note that the cross-section through x is a ring whose outer radius is x^(1/2) and whose inner radius is x^2. Thus, the cross-sectional area is A(x) = πx^(1/2)^2 - π(x^2)^2 = π(x - x^4)

Volume by slicing is V = ∫_0^1A(x) dx = ∫_0^1π(x - x^4) dx = π[x^2/2 - x^5/5] _0^1 = π(1/2 - 1/5) = (3π)/10cubic unit



(3) Consider the region contained between the graph of y = 1/x,  y = 0, x = 1, and x = 3.
This region is revolved around the y-axis. Find the volume of the resulting solid

[Graphics:HTMLFiles/test2_19.gif]

Volume by shells: V =∫_1^32π x f(x) dx = ∫_1^32π x 1/xdx = ∫_1^32π dx = π[2π x] _1^3 = 4π cubic units


(4) Find the arc length of the curve y = x^(1/3)^2  over the interval 1≤x≤8.

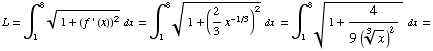
L = ∫_1^8 (1 + (f ' (x))^2)^(1/2) dx = ∫_1^8 (1 + (2/3x^(-1/3))^2)^(1/2) dx = ∫_1^8 (1 + 4/(9 (x^(1/3))^2)   )^(1/2) dx =

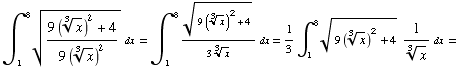
∫_1^8 (9 (x^(1/3))^2 + 4)/(9 (x^(1/3))^2) ^(1/2) dx = ∫_1^8 (9 (x^(1/3))^2 + 4 )^(1/2)/(3x^(1/3)) dx = 1/3∫_1^8 (9 (x^(1/3))^2 + 4 )^(1/2) 1/x^(1/3) dx =

1/18∫_1^8 (9 (x^(1/3))^2 + 4 )^(1/2) 6/x^(1/3) dx = 1/18∫_13^40u  ^(1/2) du = 1/18[(2u^(1/2)^3)/3] _13^40 = 1/27[u^(1/2)^3] _13^40 =

1/27 (40^(1/2)^3 - 13^(1/2)^3) = 1/27 (4040^(1/2) - 1313^(1/2)) = 1/27 (8010^(1/2) - 1313^(1/2)) units


(5) Consider the graph of y = x^3 for 0≤x≤1. This curve is revolved around the x-axis.
Compute the area of the resulting surface.

A = ∫_0^12π f (x ) (1 + f ' (x)^2)^(1/2) dx = ∫_0^12π x^3 (1 + (3x^2)^2)^(1/2) dx = 2π∫_0^1 (1 + 9x^4)^(1/2) x^3dx

2π∫_0^1 (1 + 9x^4)^(1/2) x^3dx = (2π)/36∫_0^1 (1 + 9x^4)^(1/2) 36x^3dx = π/18∫_ (1 + 9 (0)^4)^(1 + 9 (1)^4) u^(1/2) du = π/18∫_1^10 u^(1/2) du =

π/18[(2u^(1/2)^3)/3] _1^10 = π/27[u^(1/2)^3] _1^10 = π/27[10^(1/2)^3 - 1^(1/2)^3] = π/27 (1010^(1/2) - 1) units


(6) A cylindrical tank, filled with water,  is 10 meters high, and has a radius of 10 meters. Calculate the work required to pump all the water to the top of the tank. Assume that just enough work is done to overcome the force of gravity. (Recall that the density of water is 1000 kilograms per cubic meter, and the acceleration due to gravity is 9.8 meters per second per second.)

Divide the water up into n layers each of thickness Δy.
Say the kth layer is at depth y_k^* = k Δybeneath the top of the tank.
The volume of each layer is π10^2Δy = 100 πΔy.
The density of each layer is (1000)(100 πΔy) = 100000 πΔy kg.

The  kth layer must be moved a distance of y_k^*meters up to the top of the tank.
The work done in moving this layer up it approximately
W = (force)(dist) = (mass)(accel)(dist) = (100000 πΔy)(9.8)( y_k^*) = 980000 π y_k^* Δy

Total work done in removing all layers is approximately
Underoverscript[∑ , k = 1, arg3] 980000π y_k^* Δy J.

Total work done in removing all layers is exactly
Underscript[lim , n∞] Underoverscript[∑ , k = 1, arg3] 980000π y_k^* ... 747;_0^10980000πy dy = 980000π [y^2/2] _0^10 = 980000π (100/2) = 49, 000, 000π J.