_______________________________________________________________________________
Calculus  II                                                         Test #2                                              March 21, 2003

Name____________________                   R.  Hammack                                             Score ______
_______________________________________________________________________________

(1) Find the area of the region contained between the graphs of y = 1/x,  y = 1 - 1/x, and x = e.
[Graphics:HTMLFiles/test2_4.gif]
To find where the graphs intersect, we solve the equation
  1/x = 1 - 1/x
  
  2/x = 1
  
  x = 2
  
  Thus the area is ∫_2^e (1 - 1/x - 1/x) dx =∫_2^e (1 - 21/x) dx =[x - 2ln x] _2^e=(e - 2ln e) - (2 - 2ln 2)
  e - 2 - 2 + 2ln 2 = e - 4 + ln 4square units.


(2) Consider the region contained between the y axis and the curve x = y - y^2. This region is revolved around the x-axis. What is the volume of the resulting solid?

Since y = y(1-y), the y intercepts are 0 and 1. Here is a picture.

[Graphics:HTMLFiles/test2_13.gif]
Using shells,
  V = ∫_0^12π y(y - y^2) dy = 2π∫_0^1 (y^2 - y^3) dy = 2π[y^3/3 - y^4/4] _0^1 =
  
  2π[y^3/3 - y^4/4] _0^1 = 2π(1^3/3 - 1^4/4) = π/6cubic units
(3) Consider the region contained between the graphs of y = e^(-x), y = 0, x = 0, and x = 1.
This region is revolved around the x axis. Find the volume of the resulting solid


[Graphics:HTMLFiles/test2_20.gif]


Using slicing,
V =∫_0^1π (e^(-x))^2dx =∫_0^1π e^(-2x) dx =π∫_0^1 e^(-2x) dx =-π/2∫_0^1 e^(-2x)(-2) dx =-π/2∫_0^(-2) e^udu =-π/2[e^u] _0^(-2) =-π/2 (e^(-2) - e^0) =π/2 (1 - 1/e^2)cubic units.


(4)  Find the exact arc length of the curve y = 2/3x^(1/2)^3 from x = 0 to x = 3.

L = ∫_0^3 (1 + (f ' (x))^2)^(1/2) dx =∫_0^3 (1 + x^(1/2)^2)^(1/2) dx = ∫_0^3 (1 + x)^(1/2) dx =  ∫_1^4u^(1/2) du =[2/3x^(1/2)^3] _1^4 = 2/34^(1/2)^3 - 2/31^(1/2)^3 = 2/32^3 - 2/31^3 = 16/3 - 2/3 = 14/3units.
(5) Consider the graph of y = 2x^(1/2) for 0≤x≤8. This curve is revolved around the x-axis. Compute the surface area of the resulting region.

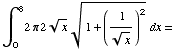
SA = ∫_0^82π f(x) (1 + (f ' (x))^2)^(1/2) dx = ∫_0^82π 2x^(1/2) (1 + (1/x^(1/2))^2)^(1/2) dx =4π ∫_0^8x^(1/2) (1 + 1/x)^(1/2) dx = 4π ∫_0^8x(1 + 1/x)^(1/2) dx =4π ∫_0^8 (x + 1)^(1/2) dx = 4π ∫_1^9u^(1/2) dx =4π [2/3x^(1/2)^3] _1^9 = 4π(2/39^(1/2)^3 - 2/31^(1/2)^3) =  4π(2/33^3 - 2/31^3) = 4π(54/3 - 2/3) = 4π52/3    =(208π)/3  square units.

(6) A basement is 10 meters long, 10 meters wide, and 5 meters deep. After a heavy rain, the basement floods to a depth of 1 meter. Calculate the work required to pump all the water out to ground level. (Recall that the density of water is 1000 kilograms per cubic meter, and the acceleration due to gravity is 9.8 meters per second per second.)

Divide the water up into n layers each of thickness Δy.
Say the kth layer is at depth y_k^* = k Δybeneath the water's surface.
The volume of each layer is (10)(10) Δy = 100 Δy.
The density of each layer is (1000)(100) Δy = 100000 Δy kg.
The  kth layer must be moved a distance of 4 + y_k^*meters up to the ground's surface.

The work done in moving this layer up it approximately
W = (force)(dist) = (mass)(accel)(dist) = (100000 Δy)(9.8)( 4 + y_k^*) = 980000( 4 + y_k^*) Δy

Total work done in removing all layers is approximately
Underoverscript[∑ , k = 1, arg3] 980000 (4 + y_k^*) Δy J.

Total work done in removing all layers is exactly
Underscript[lim , n∞] Underoverscript[∑ , k = 1, arg3] 980000 (4 + y_k^*) Δy = ∫_0^1980000 (4 + y) dy = 980000 [4y + y^2/2] _0^1 = 980000 (7/2)=4410000 J.