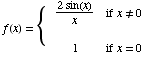___________________________________________________________________________
Calculus I Test
#1 March 8,
2004
Name____________________ R. Hammack
Score
______
__________________________________________________________________________
(1)
(a) 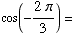 -1/2
-1/2
(b) 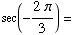
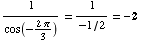
(c) Find the domain of the function 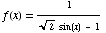 .
.
We can't have 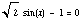 , or, in other words, we can't have sin(x) =
, or, in other words, we can't have sin(x) =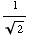 ,
,
for such values make the denominator of f 0
Now, the values of x between 0 and 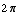 for which sin(x) =
for which sin(x) =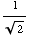 are
are 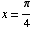 and
and 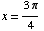 .
.
Of course, we could add any integer multiple of 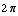 to them and still sin(x) =
to them and still sin(x) =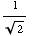 .
.
Thus the domain of f is the set 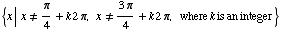
(2)
(a) Sketch the graph of the equation 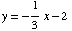 .
.
![[Graphics:HTMLFiles/test1sol_16.gif]](HTMLFiles/test1sol_16.gif)
(b) Find the equation of the line that is parallel to the graph of 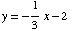 (from Part a, above) and passes through the point
(from Part a, above) and passes through the point 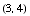 . Put your final answer in slope-intercept form, and simplify as much as possible.
. Put your final answer in slope-intercept form, and simplify as much as possible.
By point-slope formula,
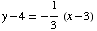
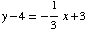
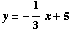
(3) Suppose 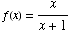 and
and 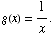
(a) 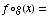
![FormBox[RowBox[{f(g(x)), =, RowBox[{(1/x)/(1/x + 1), =, RowBox[{(1/x)/(1/x &n ... x), =, RowBox[{(1/x)/((1 + x)/x), =, RowBox[{1/(1 + x), Cell[], Cell[]}]}]}]}]}], TraditionalForm]](HTMLFiles/test1sol_25.gif)
(b) 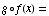
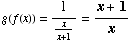
(4) Sketch the graph of a function  satisfying the following properties.
satisfying the following properties.
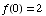 ,
, 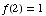 ,
, ![Underscript[lim , x2^-] f(x) = 3](HTMLFiles/test1sol_31.gif) ,
, ![Underscript[lim , x2^+] f(x) = 1](HTMLFiles/test1sol_32.gif) ,
, ![Underscript[lim , x -2] f(x) = ∞](HTMLFiles/test1sol_33.gif) ,
, ![Underscript[lim , x∞] f(x) = ∞](HTMLFiles/test1sol_34.gif) . and
. and ![Underscript[lim , x -∞] f(x) = 0](HTMLFiles/test1sol_35.gif) .
.
![[Graphics:HTMLFiles/test1sol_37.gif]](HTMLFiles/test1sol_37.gif)
Note: It's hard to draw this graph with the program I am using.
There should be a solid dot at the point (2, 1) and a hollow dot at (2, 3).
The vertical line between these points should not be there.
(5) The graph of a function 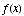 is sketched. Use this information to find the following limits.
is sketched. Use this information to find the following limits.
![[Graphics:HTMLFiles/test1sol_39.gif]](HTMLFiles/test1sol_39.gif)
(a) ![Underscript[lim , x2] 4f(x) =](HTMLFiles/test1sol_40.gif)
![Underscript[4 lim , x2] f(x) = 4 (-2) = -8](HTMLFiles/test1sol_41.gif)
(b) ![Underscript[lim , x -1] (f(x) + 2)/(f(x) + 3) =](HTMLFiles/test1sol_42.gif)
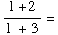 3/4
3/4
(6) Evaluate the following limits.
(a) ![Underscript[lim , x -1] (2x^3 - 4x - 5) =](HTMLFiles/test1sol_44.gif)
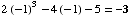
(b) ![Underscript[lim , x2] (2x^2 - 8)/(x - 2) =](HTMLFiles/test1sol_46.gif)
![Underscript[lim , x2] (2 (x^2 - 4))/(x - 2) = Underscript[lim , x2] (2 (x - 2) (x + 2))/(x - 2) =](HTMLFiles/test1sol_47.gif)
![Underscript[lim , x2] 2 (x + 2) = 2 (2 + 2) = 8](HTMLFiles/test1sol_48.gif)
(c) ![Underscript[lim , x2] (2x^2 - 8)/(x - 3) =](HTMLFiles/test1sol_49.gif)
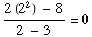
(d) ![Underscript[lim , w25] (w - 25)/(w^(1/2) - 5) =](HTMLFiles/test1sol_51.gif)
![Underscript[lim , w25] ((w^(1/2) - 5) (w^(1/2) + 5))/(w^(1/2) - 5) = Underscript[lim , w25] (w^(1/2) + 5) = 25^(1/2) + 5 = 10](HTMLFiles/test1sol_52.gif)
(e) ![Underscript[lim , x2] cos(π/(4 + x)) =](HTMLFiles/test1sol_53.gif)
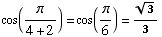
(f) ![Underscript[lim , x0] 1/(3x cot(x)) =](HTMLFiles/test1sol_55.gif)
![1/3 Underscript[lim , x0] 1/(x cos(x)/sin(x)) = 1/3 Underscript[lim , x0] 1/( ... ;0] sin(x)/(cos(x) x) = 1/3 Underscript[lim , x0] sin(x)/( x) 1/cos(x) = 1/3 (1) 1/1 = 1/3](HTMLFiles/test1sol_56.gif)
(7) This problem concerns
the function 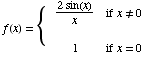
(a) 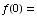 1
1
(b) ![Underscript[lim , x0] f(x) =](HTMLFiles/test1sol_59.gif)
![Underscript[lim , x0] (2sin(x))/x = 2Underscript[lim , x0] sin(x)/x = (2) (1) = 2](HTMLFiles/test1sol_60.gif)
(c) At which x
values (if any) is the function 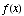 discontinuous?
Explain your answer.
discontinuous?
Explain your answer.
The function is not continuous at x
= 0, because, as the previous two answers demonstrate, ![Underscript[lim , x0] f(x) ≠f(0)](HTMLFiles/test1sol_62.gif) .
.
Thus the definition of continuity is not satisfied.
(d) Find the horizontal asymptotes (if any) of 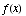 . Be
sure to explain your work.
. Be
sure to explain your work.
Note that ![Underscript[lim , x∞] f(x) = Underscript[lim , x∞] (2sin(x))/x = 0](HTMLFiles/test1sol_64.gif) (Because, while the numerator is bounded between -1 and 1, the denominator grows
without bound.)
(Because, while the numerator is bounded between -1 and 1, the denominator grows
without bound.)
Likewise the limit as x approaches negative infinity is 0.
THUS the line y = 0 is a horizontal
asymptote.
![[Graphics:HTMLFiles/test1sol_16.gif]](HTMLFiles/test1sol_16.gif)
![[Graphics:HTMLFiles/test1sol_37.gif]](HTMLFiles/test1sol_37.gif)
![[Graphics:HTMLFiles/test1sol_39.gif]](HTMLFiles/test1sol_39.gif)