_____________________________________________________________________________________
Calculus I                                                                     Test #3                                          November 24, 2003

Name____________________                              R.  Hammack                                             Score ______
____________________________________________________________________________________

(1)  Sketch the graph of the function f(x) = 2 - ln(x).
The graph of y = ln(x) is drawn dashed.
The  graph of y = -ln(x) is drawn dotted. (Previous graph reflected across the x-axis.)
The  graph of y = 2-ln(x) is drawn solid. (Previous graph moved up 2 units.)

[Graphics:HTMLFiles/T3F03Dsol_3.gif]

(2) Find the inverse of the function f(x) = 2 - ln(x).

y = 2 - ln(x)
ln(x) = 2 - y
e^ln(x) = e^(2 - y)
x = e^(2 - y)
y = e^(2 - x) (interchange x and y)

Thus, the inverse is f^(-1)(x) = e^(2 - x)

[Just as a quick check, note f^(-1)(f(x)) = e^(2 - f(x)) = e^(2 - (2 - ln(x))) = e^ln(x) = x.]

(3) Does the function  g(x) = -2x^5 - 4x^3 - 7x + 20  have an inverse? Explain.
Notice that    g ' (x) = -10x^4 - 12x^2 - 7is negative for all values of x.
This means that the graph of g(x) decreases, and never increases.
Consequently the function g(x) passes the horizontal line test, and is therefore invertible.

(4) The graph of a one-to-one function h(x) is given.  Using the same coordinate axis, sketch the graph of h^(-1)(x)
Reflecting across the line y = x, gives the following graph of the inverse, drawn in bold.

[Graphics:HTMLFiles/T3F03Dsol_17.gif]
(5) The function f(x) = x/(x + 1)is invertible.  Find the number a for which f^(-1)(a) = 3.

We seek an a for which  f^(-1)(a) = 3.
Take f of both sides to get  f(f^(-1)(a)) = f(3).
Now this becomes a = f(3) = 3/(3 + 1) = 3/4 .

(6) Solve the equation   e^(-2x) - 3e^(-x) = -2.  Hint: Notice that this has the form of a quadratic.

e^(-2x) - 3e^(-x) = -2
(e^(-x))^2 - 3 (e^(-x)) + 2 = 0
(e^(-x) - 1) (e^(-x) - 2) = 0

This equation is true if one of the two factors is 0,
that is if e^(-x) - 1 = 0 or if e^(-x) - 2 = 0.

Solving  e^(-x) - 1 = 0 gives  e^(-x) = 1;  ln(e^(-x)) = ln(1); -x = 0; x = 0
Solving  e^(-x) - 2 = 0 gives  e^(-x) = 2;  ln(e^(-x)) = ln(2); -x = ln(2); x = -ln(2)

The solutions are x = 0 and x = -ln(2).

(7)  FormBox[RowBox[{RowBox[{16, ^, RowBox[{(, RowBox[{-, 1.75}], )}]}], =}], TraditionalForm]FormBox[RowBox[{RowBox[{1, /, RowBox[{16, ^, 1.75}]}], =, 1/16^(5/4) = 1/(16^(1/4))^5 = 1/2^5 = 1/128}], TraditionalForm]
(8) ln(1/e) = -ln(e) = -1

(9)  cos^(-1)(1/2) =π/3

(10) sin(tan^(-1)(x)) == x/(1 + x^2)^(1/2)

(11) Use logarithmic differentiation to find the derivative of the function y = sin(x)^x.
y = sin(x)^x
ln(y) = ln(sin(x)^x)
ln(y) = x ln(sin(x))
d/dx[ln(y)] = d/dx[x ln(sin(x))]

(dy/dx)/y = (1) ln(sin(x)) + xcos(x)/sin(x)

dy/dx = y ( ln(sin(x)) + x cot(x))

dy/dx = sin(x)^x ( ln(sin(x)) + x cot(x))

(12)   d/dx[ x^3e^x ] =3x^2e^x + x^3e^x = e^xx^2(3 + x)

(13)   d/dx[ π^sin(x) ] =ln(π) π^sin(x) cos(x)

(14)   d/dx[   (e^(5x) + 3x)^(1/2)    + ln(x) + 4  ] = 1/2 ( e^(5x) + 3x)^(-1/2) (e^(5x) 5 + 3)    + 1/x + 0 = (5e^(5x) + 3)/(2 (e^(5x) + 3x)^(1/2)) + 1/x
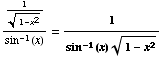
(15)   d/dx[  ln ( sin^(-1)(x) ) ] =1/(1 - x^2)^(1/2)/sin^(-1)(x) = 1/(sin^(-1)(x) (1 - x^2)^(1/2))

(16)    d/dx[tan^(-1)(1/x)] =1/(1 + (1/x)^2) (-1/x^2) = -1/(x^2 + 1)

The problems on this page are about the function f(x) = e^(-x^2/2).

(17) Find the intervals of increase/decrease.
f ' (x) = e^(-x^2/2) (-x) = -x e^(-x^2/2)

Looking at this, you can see that f '(x) is positive when x is negative and negative when x is positive.
Thus, f increases on (-∞, 0] and decreases on [0, ∞)

(18)  Find the critical points of f(x).
x = 0 is the only critical point.

(19)  Find the locations of the relative extrema of f(x), and identify them as relative maxima or minima.
Since f ' changes from  positive to negative at 0,  f  has  a relative maximum at 0.
This is the only extremum: no relative minimum.

(20)  Find the intervals on which the graph is concave up/down.

f ' (x) = e^(-x^2/2)(-x) = -x e^(-x^2/2)
f '' (x) = (-1) e^(-x^2/2) - x e^(-x^2/2) (-x) = - e^(-x^2/2) + x^2 e^(-x^2/2) = e^(-x^2/2) (x^2 - 1) = e^(-x^2/2)(x - 1) (x + 1)

      -1        1    
-----*------*-------
+ + | - - - | + + + f ' '(x)

f  is concave up on  (-∞, -1] and [1, ∞)
f  is concave down on  [-1, 1]