_____________________________________________________________________________________
Calculus I                                                                      Test #3                                             December 1, 2004

Name____________________                               R.  Hammack                                             Score ______
_____________________________________________________________________________________

(1) Find the inverse of the function f(x) = ln(x^3 + 1)

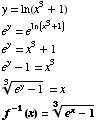
y = ln(x^3 + 1)  e^y = e^ln(x^3 + 1)  e^y = x^3 + 1  e^y - 1 = x^3  (e^y - 1)^(1/3) = x  f^(-1)(x) = (e^x - 1)^(1/3)


(2)  Is the function g(x) = e^x + e^(-x)  invertible or not?  Explain.

No.  It's not one-to-one:
g(1) = e^1 + e^(-1), and g(-1) = e^(-1) + e^1,
so g(1) = g(-1).
It fails the H.L.T.


(3) Find the equation of the tangent line to the graph of  y = sin^(-1)(x) at the point where x = 3^(1/2)/2.

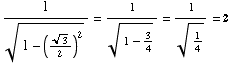
Slope at x is y ' =1/(1 - x^2)^(1/2). Thus the slope of the tangent is 1/(1 - (3^(1/2)/2)^2)^(1/2) = 1/(1 - 3/4)^(1/2) = 1/1/4^(1/2) = 2

Point of tangency is (3^(1/2)/2, sin^(-1)(3^(1/2)/2)) = (3^(1/2)/2, π/3)

Point-Slope formula: y - π/3 = 2 (x - 3^(1/2)/2)

ANSWER: y = 2x - 3^(1/2) + π/3


(4)  Solve the equation  ln(x^2 + 5x + 7) = 0.

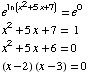
e^ln(x^2 + 5x + 7) = e^0  x^2 + 5x + 7 = 1  x^2 + 5x + 6 = 0  (x - 2) (x - 3) = 0
SOLUTIONS: 2, 3

(5) Simplify each expression as much as possible.

(a)  FormBox[RowBox[{RowBox[{(1/4), ^, RowBox[{(, RowBox[{-, 1.5}], )}]}], =}], TraditionalForm]FormBox[RowBox[{RowBox[{((1/4)^(-1)), ^, 1.5}], =, RowBox[{RowBox[{4, ^, 1.5}], =, 4^(3/2) = (4^(1/2))^3 = 2^3 = 8}]}], TraditionalForm]

(b)  sin^(-1)(-1/2) =-π/6

(c)  log ( 1 ) =0

(d)  4^(2log_4(5)) =4^log_4(5^2) = 25

(e)  sec^(-1) ( ln(e^3e^(-1)) ) =sec^(-1) ( ln(e^(3 - 1)) ) = sec^(-1) ( ln(e^2) ) = sec^(-1)(2) = π/3

(6)   The graph of the derivative of a function f is given. [Graphics:HTMLFiles/T3F04D_24.gif]
In each case, indicate whether the ? should be replaced with the symbol <, >,  or =.

(a)      f(1)   ?     f(3) ANSWER: > , because f decreases between 1 and 3 (its derivative is negative there).

(b)    f '(1)   ?    f '(3)  ANSWER: =, by reading straight from the graph.

(c)    f "(1)   ?    f "(3) ANSWER: <, by looking at slope on the graph of f '

(7) Find the derivatives.

(a)   d/dx[ 6^x ] =ln(6) 6^x

(b) d/dx[log(x)] = 1/(ln(10) x)

(c) d/dx[ ln(x)] = 1/x

(d)  d/dx[ e^(4x + ln(x))] = e^(4x + ln(x))(4 + 1/x)

(e) d/dx[ tan^(-1)(x) ln(tan(x))] =1/(1 + x^2) ln(tan(x)) + tan^(-1)(x) sec^2(x)/tan(x)

(f) d/dx[ln(x)/e^x] = (1/xe^x - ln(x) e^x)/(e^x)^2 = e^x (1/x - ln(x))/(e^x)^2 = (1/x - ln(x))/e^x

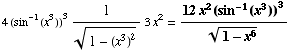
(g)  d/dx[ (sin^(-1)(x^3))^4 ] =4 (sin^(-1)(x^3))^31/(1 - (x^3)^2)^(1/2) 3x^2 = (12x^2(sin^(-1)(x^3))^3)/(1 - x^6)^(1/2)

(h) d/dx[  x^x] = x^x (ln(x) + 1), using logarithmic differentiation, as below.

y = x^x  ln(y) = ln(x^x)  ln(y) = x ln(x)  d/dx[ln(y)] = d/dx[x ln(x)]  1/yy ' = ln(x) + x1/x  y ' = y (ln(x) + 1)  y ' = x^x (ln(x) + 1)

(8)  Consider the function f(x) = x^4 + 8x^3 + 18x^2 - 8.

(a)    List all critical points of f.

f ' (x) = 4x^3 + 24x^2 + 36x = 4x(x^2 + 6x + 9) = 4x(x + 3)^2
From this you can read off the critical points as 0 and -3

(b)     Find the intervals on which f increases/decreases.
   -3      0
---|------|-----
- - - - - - + + +f '(x)

f increases between 0 and infinity.
f decreases between negative infinity and 0

(c)     Find the intervals on which f  is concave up/down.

f '' (x) = 12x^2 + 48x + 36 = 12 (x^2 + 4x + 3) = 12 (x + 1) (x + 3)

   -3      -1
---|------|-----
++ - - -  + + +f ''(x)

f is concave down on [-3,-1]
Elsewhere, f is concave up

(d)    Locate and identify all extrema of f .

By first derivative test (see part b above) there is a relative minimum at x = 0.
There is no relative maximum.

(e)    List the locations (x-values) of all inflection points of f.

By part c above, the locations are -3 and -1.