_____________________________________________________________________________________
Calculus I Test
#2 November
3, 2004
Name____________________ R. Hammack Score
______
_____________________________________________________________________________________
(1) Suppose f(x)
is a function for which the following limits hold.
![Underscript[lim , w0] (f(w) - f(0))/(w - 0) = -1](HTMLFiles/T2F04A_1.gif)
![Underscript[lim , w1] (f(w) - f(1))/(w - 1) = 5](HTMLFiles/T2F04A_2.gif)
![Underscript[lim , w2] (f(w) - f(2))/(w - 2) = 0](HTMLFiles/T2F04A_3.gif)
![Underscript[lim , w5] (f(w) - f(5))/(w - 5) = 3](HTMLFiles/T2F04A_4.gif)
Based on this information, answer the following questions.
(a) Is there a value of x
at which the tangent line to the graph of y
= f(x)
is horizontal? If so, what is x?
The third limit says f '(2)
= 0, so x
= 2 is such a value.
(b) Find the slope of the tangent line
to the graph of y = f(x) at
the point where x = 5.
The fourth limit says f
'(5) = 3, so the slope is 3.
(c) Suppose you also know
that f(0) = 5. Find the
equation of the tangent line to the
graph of y = f(x) at
the point where x = 0.
The first limit says f '(0)
= -1, so the tangent line has slope -1 and y-intercept 5. It's equation is thus
y
= -x
+5
(2) The graph of a function g(x)
is illustrated below. Sketch the graph of g
'(x).
![[Graphics:HTMLFiles/T2F04A_5.gif]](HTMLFiles/T2F04A_5.gif)
![[Graphics:HTMLFiles/T2F04A_6.gif]](HTMLFiles/T2F04A_6.gif)
(3) If  , find
, find
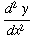
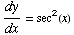
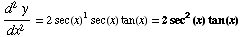
(4) ![d/dx[ 2x^9 - x + 6 ] =](HTMLFiles/T2F04A_11.gif)
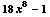
(5) ![d/dx[ 1/x + 3/x^(1/2)] =](HTMLFiles/T2F04A_13.gif)
![d/dx[ x^(-1) + 3x^(-1/2)] = -x^(-2) + 3 (-1/2) x^(-3/2) = -1/x^2 - 3/(2x^(1/2)^3)](HTMLFiles/T2F04A_14.gif)
(6) ![d/dx[ x^2cot(x)] =](HTMLFiles/T2F04A_15.gif)
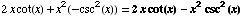
(7) ![d/ds[ (4x + 2)/cos(x)] =](HTMLFiles/T2F04A_17.gif)
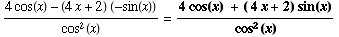
(8) ![d/dx[ sin(1/x)] =](HTMLFiles/T2F04A_19.gif)
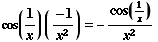
(9) ![d/dx[(x^2 + 9 )^(1/2)] =](HTMLFiles/T2F04A_21.gif)
![d/dx[(x^2 + 9)^(1/2) ] = 1/2 (x^2 + 9)^(-1/2) (2x) = x/(x^2 + 9)^(1/2)](HTMLFiles/T2F04A_22.gif)
(10) ![d/dx[ x sec ( π x ) ] =](HTMLFiles/T2F04A_23.gif)
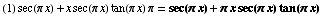
(11) ![d/dx[ sin^2(x) (2x + 1)^3 ] =](HTMLFiles/T2F04A_25.gif)
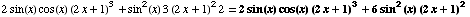
(12) ![d/dx[ tan^3(x^(1/2))] =](HTMLFiles/T2F04A_27.gif)
![d/dx[( tan(x^(1/2)))^3] = 3 ( tan(x^(1/2)))^2d/dx[ tan(x^(1/2))] = 3 tan^2(x^(1/2)) sec^2(x^(1/2)) 1/(2x^(1/2))](HTMLFiles/T2F04A_28.gif)
(13) Find the values
of x at which the tangent to the graph
of 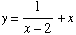 is
horizontal.
is
horizontal.
If the tangent is horizontal, its slope 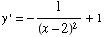 must be 0, so we need to solve
must be 0, so we need to solve
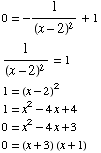
Answer: x
= 3 and x
= 1
(14) An object, moving on
a straight line, is at a distance of 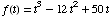 feet
from a stationary point on the line at time t
seconds.
feet
from a stationary point on the line at time t
seconds.
(a) Find the function for
the object's velocity at time t.
Velocity at time t is
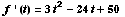 feet per second
feet per second
(b) At what time(s) is the
object's velocity 5 feet per second?
When f '(t)
= 5.
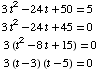
Answer: when t
= 3 seconds and t
= 5 seconds
(15) At which values of x
do the graphs of 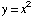 and
and 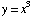 have
the same slope?
have
the same slope?
![2x = 3x^2 2x - 3x^2 = 0 FormBox[RowBox[{x (2 - 3x), =, RowBox[{0, Cell[]}]}], TraditionalForm]](HTMLFiles/T2F04A_37.gif)
Answer: x
= 0 and x
= 2/3
(16) Find the slope
of the tangent to the graph of the equation ![2 2 FormBox[RowBox[{ , Cell[TextData[{Cell[BoxData[x - y = x y - 1]], }]]}], TraditionalForm]](HTMLFiles/T2F04A_38.gif) at the point (3, 2).
at the point (3, 2).
![d/dx[x^2 - y^2] = d/dx[x y - 1] 2x - 2y y ' = (1) y + x y ' - 0 2x - y = x y ... 371; y ' = (2x - y)/(x + 2y) y ' | _ ((x, y) = (3, 2)) = (2 (3) - (2))/(3 + 2 (2)) = 4/7](HTMLFiles/T2F04A_39.gif)
(17) A stone dropped into
a still pond sends out a circular ripple whose radius increases at a rate of
2 feet per second. How rapidly is the area enclosed by the ripple
increasing 10 seconds after the stone is dropped?
Let r be the radius of the ripple,
and let A be its area.
We know 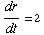
We want 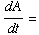 ?
?
r and A
obey the equation 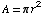 (area of a circle). Differentiating both sides with respect to time
t,
(area of a circle). Differentiating both sides with respect to time
t,
![d/dt[A] = d/dt[π r^2] dA/dt = 2π r dr/dt dA/dt = 2π r (2) dA/dt = 4π r](HTMLFiles/T2F04A_43.gif)
10 seconds after the stone is dropped, the ripple's radius is (10 sec)(2 ft/sec)
= 20 feet.
Plugging this in, we get 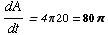 square feet per second.
square feet per second.
![[Graphics:HTMLFiles/T2F04A_5.gif]](HTMLFiles/T2F04A_5.gif)
![[Graphics:HTMLFiles/T2F04A_6.gif]](HTMLFiles/T2F04A_6.gif)
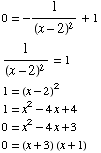
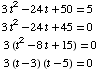
![2x = 3x^2 2x - 3x^2 = 0 FormBox[RowBox[{x (2 - 3x), =, RowBox[{0, Cell[]}]}], TraditionalForm]](HTMLFiles/T2F04A_37.gif)
![d/dx[x^2 - y^2] = d/dx[x y - 1] 2x - 2y y ' = (1) y + x y ' - 0 2x - y = x y ... 371; y ' = (2x - y)/(x + 2y) y ' | _ ((x, y) = (3, 2)) = (2 (3) - (2))/(3 + 2 (2)) = 4/7](HTMLFiles/T2F04A_39.gif)
![d/dt[A] = d/dt[π r^2] dA/dt = 2π r dr/dt dA/dt = 2π r (2) dA/dt = 4π r](HTMLFiles/T2F04A_43.gif)