Calculus I
Test #2
October  22, 2001
Name____________________
R.  Hammack
Score ______


(1)   Suppose   f(x) = 1/(2x).     Use the limit definition of the derivative to find  f '(x).
  
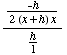
f '(x) =  Underscript[lim , h0](f(x + h) - f(x))/h= Underscript[lim , h 0](1/(2 (x + h)) - 1/(2x))/h = Underscript[lim , h0](x - (x + h))/(2 (x + h) x) /h= Underscript[lim , h0] ( -h)/( 2 (x + h) x) /h/1

=  Underscript[lim , h0] ( -  h)/( 2 (x + h) x) 1/h=  Underscript[lim , h0] ( -  1)/( 2 (x + h) x)= -1/(2x^2)

  


(2) Find the derivatives of the following functions. You may use any applicable rule.
  
(a)    f(x) = 4x^10+ 3x^3+   π^2
f '(x) = 40 x^9+ 9x^2
  
(b)   f(x) = (x + sin x)/(cos x)

f ' (x) =  ((1 + cos x) cos x - (x + sin x) (-sin x))/(cos ^2x)

(c)  y = x tan(x)
dy/dx = (1)tan x + x sec^2x = tan x + x sec^2x


(d) d/dx[ 25 + cos( x ^4) ] = 0 + d/dx[  cos( x ^4) ] = -sin ( x ^4) 4x^3= -4x^3sin ( x ^4)


(e) d/dx[ (x^2 + 4)^(1/2) ] = d/dx[ (x^2 + 4)^(1/2) ] = 1/2(x^2 + 4)^(-1/2)(2x) = x/(x^2 + 4)^(1/2)


(3) Suppose f(x) equals the number of dollars it costs to erect an x-foot-high transmitting tower.
(a) What are the units of f '(x)?
dy/dx = dollars per foot

(b) Suppose that f '(100) = 105.    Explain, in ordinary English, what this means.
It will cost $105 to build the 101st foot

(4) This problem concerns the function f that is graphed below

[Graphics:HTMLFiles/2F01sol_39.gif]

(a)    Sketch the graph of f '(x). (Use the same coordinate axis)

(b)    Suppose g(x) = sin(f(x)). Find g '(4).
By the chain rule,  g '(x) = cos( f(x) ) f '(x),
so g '(4) = cos(f(4)) f '(4) = cos(1)(0) = 0

(c)   Suppose h(x) = 4 + x^2+ x^2f(x).   Find h'(2).
h '(x) = 2x + 2x f(x) + x^2f '(x),
so h '(2) = 2(2) + 2(2)(f(2)) + 2^2f '(2) =  2(2) + 2(2)(1.5) + 2^2(-1) = 4 + 6 - 4 = 6



(5) Sketch the graph of a function  f  whose derivative has the following properties:
f(0) = 2,     f '(0) = 0,    f '(3) = 0,   and  f '(x) ≤ 0 for all values of x.

  [Graphics:HTMLFiles/2F01sol_45.gif]

(6) Consider the function  f(x) = x + x^(1/2)

(a) Find the slope of the tangent line to the graph of f at the point where x = 4.
f '(x) = 1 +1/(2x^(1/2)), thus the slope we seek is f '(4) = 1 +1/(24^(1/2))= 1+1/4 = 5/4

(b) Find the equation of the tangent line to the graph of f at the point where x = 4.
The slope is 5/4 (from part a), and the line passes through the point (4, f(4)) = (4, 6).
Using the point-slope formula:
y - 6 = 5/4(x - 4)
y - 6 = 5/4 x - 5
y = 5/4 x + 1


(7) Find all values of x for which the slope of the tangent to the graph of   y = sin x   at the point   x   is  1/2 .

Slope = dy/dx = cos x, so we are looking for all values of x for which cos x = 1/2.
Looking at the unit circle, we see that these values of x are x = π/3 + k2π  and x = -π/3 + k2π , where k is an integer.


(8)  Find the slope of the tangent to the graph of   tan(xy) = y^2 at the point (π/4,  1).
d/dx[tan(xy) ]    = d/dx[y^2]

sec^2(xy) (y + xdy/dx) = 2ydy/dx

sec^2(xy) y + sec^2(xy) xdy/dx = 2ydy/dx

sec^2(xy) xdy/dx   - 2ydy/dx = -sec^2(xy) y

dy/dx (sec^2(xy) x   - 2y) = -sec^2(xy) y

dy/dx = (-sec^2(xy) y )/(sec^2 (xy) x   - 2y)

dy/dx | _ ( (x, y) = (π/4, 1)) = -sec^2(π/4) /(sec^2(π/4) π/4   - 2) = -2/(2 (π/4) - 2) = -1/((π/4) - 1) = -4/(π - 4)= 4/(4 - π )

(9) Suppose a 10-foot-long ladder is sliding down a wall in such a way that the base of the ladder moves away from the wall at a constant rate of 2 feet per second.  How fast is the top of the ladder moving down the wall when it is 6 feet above the floor?

Let x be the distance from the wall to the base of the ladder. Let y be the height of the top of the ladder.
We know dx/dt= 2, and we want to find dy/dt.
By the Pythagorean Theorem, x^2 + y^2 = 10^2. Differentiating both sides with respect to t:
d/dt[ x^2 + y^2]    = d/dt[100]

2xdx/dt + 2ydy/dt = 0

2x + ydy/dt = 0,   so       dy/dt = (-2x)/y

Now use the Pythagorean Theorem again to find that x = 8 when y = 6.
Then dy/dt = (-2x)/y= (-2 (8))/6 = -8/3 feet per second .