The question "What is life?" has been around for some time. There is an impressive list of great minds that tackled the question. In spite of this, it never has been answered in any definitive way. Robert Rosen, a student of Nicholas Rashevsky and a product of the Mathematical Biology program at the University of Chicago started one line of research that grappled with the question in the late 1950's. It is worth examining the progression, which lead Bob Rosen to realize that he was dealing with a poorly posed question and that when rephrased, the question had an earthshaking answer.

The answer was earthshaking not so much due to its information content but more so due to the process by which it was answered. This process and its really revealing ramifications will be the subject of this review. It is no easy task to try to say these things in Bob Rosen's stead, and you will suffer from having to hear a surrogate. On the other hand, to see beyond where anyone has seen before has often necessitated standing on the shoulders of giants.

What we will examine here is the entire epistemological basis for modern science. We will examine it with a view that, in itself, is a product of that very examination. And, thus, from the onset, we will be forced to stop every step of the way in order to remind ourselves that what we are doing is only effective if it is changing even as we do it.

Why so bold a goal? Because anything short of that easily and deceptively lapses back into well worn tracks even if dressed to seem new and different. What Robert Rosen discovered had that effect on him, and, as he wrote and spoke over the years, it began to have an effect on some of us. The path we are about to traverse is very difficult. It was even more difficult for Bob, for as he saw, he had to communicate what he saw. This is difficult enough with new ideas even when they nicely extend the ideas upon which they are built. It is far more difficult when the new ideas radically change that perspective.

Now we will move on to the subject at hand. The role of the machine metaphor in science goes back to Descartes. Newton and those who followed built it into what has become modern science. The success of this world-view was so great that it became as strong as any of the other belief structures we might identify as religions. In this case, however, science was to liberate us from superstition and myth and to give us a basis for evaluating those things that were to be candidates for truth.

Hence physics dealt with the fundamental laws of nature and chemistry and biology were to use these laws to deal with specific applications of the general laws physics discovered. In other words, the relation of physics to biology, in particular, is that of the general to the special. Rosen was able to see that, in fact, this was a prison for our thought and an extreme handicap to our understanding. It was a legacy of the machine metaphor. How could this be? It is so because the world of the machine is a "simple" world. Its laws and inhabitants are simple machines or mechanisms. What if the objects in chemistry and biology are not that simple? Then we must reduce them to subunits that are. By this reductionist path we will learn all that there is to learn about the real world. Robert Rosen discovered that this approach was a dead end! He discovered that when the reduction is performed, something real and necessary is lost and in a way which made it unrecoverable. This profound realization turned the ontology of our world upside down! It isn't the atoms and molecules that are at the hard core of reality, it is the relations between them and the relations between them and things called processes which are at the core of the real world!

There is much to this discovery and we will only be able to have a taste of it. In that tasting we will examine the modeling relation that is the key to our own ongoing examination of what we are doing as we do it! We will examine the alternative to a mechanistic world, a world of processes and causes. A world ever changing and yet a world more rational than the sterile world of machines. Finally, we will utilize this new way of seeing to repose the question about life and answer it.

The goal of this paper is to reveal to the reader a view of science that has the potential for changing its direction in the most profound way since the time of Descartes. The example used to convey this view is the issue of life: "Life itself", to steal the title of Robert Rosen's book on this subject. This potential change has an historical timeliness since it is happening during a time when much else calls for it. There clearly will not be an opportunity to pursue that digression here, due to space limitations, but it needs to be pursued. In order to have any hope of achieving so bold a goal, it will be necessary to present a skeleton with the hope that meat can be added to the bones by those interested enough to go on with the thoughts. In this case, even a skeletal presentation requires that the reader be willing to suspend certain ideas about science which are usually taken as "fundamental". The whole notion of what is fundamental is open to examination here. That, in fact, is how to begin.

In order to be able to deal with some very confusing issues, it is necessary to formulate just what it is we think we are doing when we carry out this function called "science". In a very real sense what we mean by science is the ultimate version of what humans do quite regularly, namely the perception of their world. The "perception of the world" is merely the way humans turn sensory information into awareness. What is that all about? Here's one idea that will serve the purpose for this discussion (Fischler and Firschein, 1987, 233)

This simple observation is fraught with meaning. So much meaning that it is worth examining its implication in some detail.

1.1.1 The traditional view of science: the role of measurement

Science is the way we have developed to avoid our perception 's being "creative" in the above sense. Science is a creative endeavor, but the creativity must not cloud our sensation of the world in any way. In order to accomplish this we have developed a methodology that is supposed to prevent our minds from tampering with the sensory information. We call this measurement. Often the methodology that insures this "objective" view of the world is called the scientific method. It should be clear that our notion of objectivity is intimately associated with this concept.

Since Rosen devoted at least an entire book to this topic (Rosen, 1978), it will be necessary to give a summary here. The process of measurement is something Rosen saw as related to a number of other important concepts that will be involved in this development. Along with measurement are recognition, discrimination, and classification. It is impossible (even if desirable to some) to reduce the issue of measurement to something independent of these other factors as we shall see.

Two propositions are axiomatic in the formalization of the role of measurement in our perception. Bear in mind that what is being developed here is a way of dealing with the traditional view of science.

PROPOSITION 1: "The only meaningful physical events which occur in the world are represented by the evaluation of observables on states."

PROPOSITION 2: "Every observable can be regarded as a mapping from states to real numbers."

Rosen warns us that the consequences of adopting these propositions as a mode of operation are very profound. They are, however, the kind of price science is willing to pay for its claim to be able to minimize the role of the conscious mind in the perception of sensory information. It should be clear that the act of measurement is an abstraction. We will return to this point shortly. The trade off is in the belief that, by making this abstraction, the "world" has qualities which, when measured properly, are common to all objective observers. A quote from Fundamentals of Measurement sums it all up very well:

The modeling relation is based on the universally accepted belief that the world has some sort of order associated with it; it is not a hodge-podge of seemingly random happenings. It depicts the elements of assigning interpretations to events in the world . The best treatment of the modeling relation appears in the book Anticipatory Systems (Rosen, 1985, pp 45-220). Rosen introduces the modeling relation to focus thinking on the process we carry out when we "do science". In its most detailed form, it is a mathematical object, but it will be presented in a less formal way here. It should be noted that the mathematics involved is among the most sophisticated available to us. In its purest form, it is called "category theory" [Rosen, 1978, 1985, 1991]. Category theory is a stratified or hierarchical structure without limit, which makes it suitable for modeling the process of modeling itself.

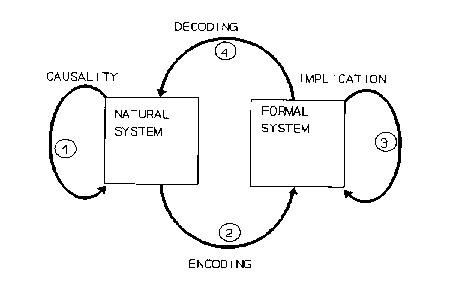
Figure 1. The modeling relation.

Figure 1 represents the modeling relation in a pictorial form. The figure shows two systems, a natural system and a formal system related by a set of arrows depicting processes and/or mappings. The assumption is that when we are "correctly" perceiving our world, we are carrying out a special set of processes that this diagram represents. The natural system is something that we wish to understand. In particular, arrow 1 depicts causality in the natural world. This idea will need some additional explanation further on. On the right is some creation of our mind or something our mind uses in order to try to deal with observations or experiences we have . The arrow 3 is called "implication" and represents some way in which we manipulate the formal system to try to mimic causal events observed or hypothesized in the natural system on the left. The arrow 2, is some way we have devised to encode the natural system or, more likely select aspects of it (having performed a measurement as described above), into the formal system. Finally, the arrow 4 is a way we have devised to decode the result of the implication event in the formal system to see if it represents the causal event's result in the natural system. Clearly, this is a delicate process and has many potential points of failure. When we are fortunate to have avoided these failures, we actually have succeeded in having the following relationship be true:

When this is true, we say that the diagram commutes and that we have produced a model of our world.

Please note that the encoding and decoding mappings are independent of the formal and/or natural systems. In other words, there is no way to arrive at them from within the formal system or natural system. This makes modeling as much an art as it is a part of science. Unfortunately, this is probably one of the least well appreciated aspects of the manner in which science is actually practiced and, therefore, one which is often actively denied. It is this fact, among others, which makes the notion of objectivity as defined above have a very shaky foundation. How could such a notion become so widely accepted?

1.14 The Newtonian Paradigm and the modeling relation

Traditional science as described above is the result of many efforts, yet it has a core set of beliefs underlying it which Rosen refers to as The Newtonian Paradigm. There is no strict definition of what this is, but it is the entire attitude and approach that arises after Newton introduced his mechanics , especially, his mathematical approach. It certainly embodies the ideas of Descartes and the heliocentrists, for example. It also embodies all of the changes brought about by quantum mechanics. It is so much what modern science is that it could almost be used as a synonym. For these reasons, it has had a profound effect on our perception. It is so powerful a thought pattern that it has seemed to make the modeling relation superfluous. For The Newtonian Paradigm, all of nature encodes into this formal system and then can be decoded. All our models come from this one largest model of nature. In the modeling relation, the formal system lies over the natural system and the encoding and decoding are masked so that the formal system is the real world . The fact that this is not the case is far from obvious to most. The task then, is to understand why.

1.1.5 Putting it all together: the modeling relation is the key

Rosen calls the results of our sensory experiences as they manifest themselves in our awareness percepts. If all we did were to use measurement to objectively become aware of what our senses pick up, the situation would be simple. We would be like a piece of magnetic tape or computer memory filing away this information as it comes in. The key word in the definition of percept is awareness. There is more to that awareness than a mere entering into memory. The first thing we would have to do, even to merely file the information correctly is to discriminate and classify. In short, we form relations between percepts. What is fascinating about this is the fact that these relationships between percepts can be matched by relationships between objects used in the formal system. Here is the place where semiotics and other aspects of our thought process get mixed into the process in an irreducible way (Dress, 1998,1999).

The confusion that arises from the failure to recognize this process at work is immense. Rosen's whole concept of the modeling relation is the explanation for why words like complexity and emergence have become so popular. The suppression of awareness of the process by the Newtonian Paradigm resulted in some real problems, surprises and errors. It was not until there was widespread recognition, consciously or unconsciously, that this paradigm was inadequate that these words became widely talked about. The world as modeled by the Newtonian Paradigm was but one possible picture of the world. Rosen named this world the world of simple systems or mechanisms.

There is another world, namely the one containing the natural systems we seek to understand, which can not be totally captured by the Newtonian model. This world, in fact, can not be captured by any number of formal systems except in the limit of all such systems. The name of this world is the world of the complex. Emergence then is the phenomenon of being surprised when the real world doesn't conform to the simple model, in other words, the discovery of its complexity. Since the entire real world is complex, discussions of degrees of complexity refer to the nature and number of formal systems being used to create models within the modeling relation. Unless this is realized, the amount of confusion generated trying to classify things by their complexity can be immense. There are many other definitions of complexity (Horgan, 1996 ) that exemplify this confusion.

Given the modeling relation and the detailed structural correspondence between our percepts and the formal systems into which we encode them, it is possible to make a dichotomous classification between various models of the real world. These models are either simple mechanisms or complex systems. It then becomes possible to formulate the "what is life" question in an entirely new way, one which leads immediately to an answer.

The answer to this question is implicit in the discussion of the modeling relation above. In order to make it explicit, there are some very important epistemological prerequisites that must be accepted. This acceptance may be for the sake of the argument or it may be a total change in direction for anyone seeking to do science in the future. The case will be made systematically.

The discussion of the modeling relation established that the world of the Newtonian Paradigm is a world of simple mechanisms or machines. As Rosen began to apply this idea to the world, he saw that it had an extremely general categorical application. To say it as concisely as possible, this world was the world described by Church's Thesis. In other words, it is a totally syntactic world, one that can be constructed by algorithms and simulated. It has a largest model from which all other models can be derived. Its models have the nature that analytic models and synthetic models are the same. This leads to their reducibility, the whole is merely the sum of their parts. The machine which becomes a prototype of this general description is the Universal Turing Machine. Thus all of computer simulation, Artificial Life and Artificial Intelligence are part of this world. The fact that these are not part of the world of complex systems is directly contradictory to the claims being made by most that have espoused the "new science" of complexity. Church's Thesis says that all effective systems are computable. Rosen's work says that church's thesis is false. There is no middle ground here. The difference is one of profound epistemological significance. There is still another distinction that must wait until the subject of causality and entailment is discussed. For it is in that discussion that the most profound epistemological change will be realized. Before delving into that matter we will compare complex systems to machines.

A complex system falls outside the formalism called the Newtonian Paradigm. That is not to say that complex systems can not be seen as machines for limited kinds of analysis. This is , in fact, what traditional science does. Using Rosen's general characteristics to separate the two kinds of objects, we see that complex systems contain semantic aspects which can not be reduced to syntax. Therefore they are not simulatable even though, when viewed as machines, the machine model is simulatable. They have no largest model from which all other models can be derived. This is simply because complex systems, by their very nature, require multiple distinct ways of interacting with them to capture their qualities. Their models are now distinct. Analytic models, which are expressed mathematically as direct products of quotient spaces are no longer equivalent to synthetic models which are built up from disjoint pieces as direct sums. Using this formulation every synthetic model is an analytic model, but there are analytic models which are not synthetic models. In other words, these analytic models are not reducible to disjoint sets of parts. This is a most profound distinction and requires some elaboration, for in it lies the essence of the failure of reductionism. In the machine, each model analytic or synthetic, is formulated in terms of the material parts of the system. Thus any model will be reducible and can be reconstructed from its parts.

This is not the case in a complex system. There are certain key models which are formulated in an entirely different way. These models are made up of functional components which do not map to the material parts in any one to one manner. The functional component itself is totally dependent on the context of the whole system and has no meaning outside that context. This is why reducing the system to its material parts loses information irreversibly. This is a cornerstone to the overall discovery Rosen made. It captures a real difference between complexity and reductionism which no other approach seems to have been able to formulate. This distinction makes it impossible to confuse computer models with complex systems. It also explains how there can be real "objective" aspects of a complex system that are to be considered along with the material parts, but which have a totally different character. Finally, this distinction between functional components and parts can be realized with an appropriate formalism. This formalism is called Relational after Rashevsky's Relational Biology (Rashevsky, 1954).

At the risk of understating the case, once one realizes that the model for the world of simple machines works so very well for machines, but only for machines, the possibility of science extending its boundaries and encompassing the myriad of self-referential and other heretofore 'forbidden" events becomes very exciting. The question then becomes one of the meaning of the concept of science in the first place.

The traditional notion of science focuses on a method in a broad sense of the word. The alternative has always been to consider a science of content. It can be argued that the latter is really the more "objective" since it is capable of shedding the bias toward a single method and will accept "truth" independent of the method for obtaining it. Clearly, this is a topic for much more discussion than is warranted here. What is important here is to demonstrate that there are valid methods that were excluded by traditional science and that can lead to important truths if allowed to be considered.

Traditional science teaches that the proper way to formulate questions is to ask "how?". This fits the needs of the world of simple mechanisms very well, since what needs to be known is "how it works?" In fact since the modeling relation has been frozen as suggested before, all that is left is to go out and make measurements, hence the huge over-emphasis on empiricism. It is often stated that one of the benefits of the Cartesian/Newtonian worldview is the liberation from the old views of Aristotle. Yet we know that for his time Aristotle did reasonably well in reasoning out answers to questions about his world. Is it possible that a baby was thrown out with the bath water when he was declared outmoded? Aristotle was fond of asking "why?" questions about the world. His answers fell into four causes:

• Material Cause
• Efficient Cause
• Formal or Formative cause
• Final Cause

To answer the question "why a house" we might say that the material it is built of is its material cause. The builders who constructed it are the efficient cause and the formal cause is the blueprint that was the plan for the house. Without taking the space to illustrate it in detail, it will be merely stated that the Newtonian Paradigm can easily be shown to yield to this kind of causal analysis for the first three causes listed above. Rosen shows that each of the first three causes has a special meaning in Newtonian dynamics. Each one enters that paradigm in a separate and distinguishable manner. The fourth cause is never allowed to be considered. What is the final cause for this house? That someone needed a dwelling place. This open acknowledgement of "purpose", closely related to but distinct from what biologists call teleology, is not something "good" science is about. If we look at the other side of the coin we have been minting, we see some interesting contrasts.

Complex systems , as we have developed the concept, are merely real systems for which we want richer interactions than the limited kind dictated by the Newtonian paradigm. In such cases, we use the modeling relation to find models based on additional formal systems which are more than mere derivations of the Newtonian Paradigm. One of the first steps in developing such a formalism is the choice of question we pose about the real world. If we choose to replace "how?" questions which are only appropriate for the mechanistic approach with "why?" questions we see that there are four answers available to us. What is both interesting and consistent with the idea that Rosen's categories of simple vs. complex are useful, is the observation that in complex systems the causes behave in totally different ways. Besides the fact that complex systems always involve all four causes, they are generally mixed and can not be separated as they can in machines.

In this context, final cause carries a connotation of anticipation with it. This idea is highly developed as a characteristic of complex systems by Rosen.. What is important for this discussion is to notice the way in which causes become mixed in a complex system. This is in distinction to the way they stand separate in simple mechanisms (Rosen, 1985, 1991). This demonstrates an interesting consistency in the distinction between the machine and the complex, since the causality argument was independent from the other distinctions between simple and complex systems, yet it fits that distinction very well.

With a little more imagination we can construct interesting descriptions of systems this way in which, as in the example of the house above, final cause carries a connotation of anticipation with it. This idea is highly developed as a characteristic of complex systems by Rosen. It is important for this discussion to note the way in which causes become mixed in a complex system. This is in distinction to the way they stand separate in simple mechanisms (Rosen, 1985, 1991). The way that final cause and anticipation are realized is in the ability of complex systems to incorporate a model of their environment into their behavior. This allows them to anticipate future events and to also correct their behavior as new information sheds light on the anticipatory process. One simple example of such a system at the level of metabolic processes has a mechanistic realization that has been examined in some detail (Rosen, 1985, pp 349-354; Mikulecky, 1993; Prideaux, 1995)

Another facet of final cause being acknowledged is the recognition that future events can cause present behavior. In the case of final cause and anticipation, the causality flows backwards so to speak. What would have once sounded like mysticism becomes perfectly reasonable in a dynamic system. The nature of causality introduces this new directionality in time in a way that the Newtonian Paradigm made impossible.

Much later, independently, a new modeling method was developed which recognized explicitly that topological connectedness in a system was as important, if not more important than the usual mechanistic description of how its parts worked. This new approach was the use of electrical network analogs in a special way called Network Thermodynamics (Peusner, 1970, 1986; Oster, Perelson and Katchalsky, 1973, Mikulecky, 1993). What became clear from the role of topology in this mechanistic formalism was that organization had its own contribution to system properties. Furthermore, much of system behavior once attributed to molecular mechanics and other mechanistic explanations could be shown to be independent of those mechanisms. Among them was the Onsager Reciprocal Relations in non-equilibrium thermodynamics and Tellegen's theorem. In fact, the theory of n-ports made network theory and non-equilibrium thermodynamics analogs. It was easy to manipulate n-port networks in a way that kept the physical description of the network element constant while network topology alone was being altered to demonstrate that entirely new systems behavior would result. It would be remiss to fail to mention one of the most impressive uses of topological reasoning in science, namely Carotheodry's proof of the second law of thermodynamics. (for more details on all of these see Mikulecky, 1993)

The trivial distinction in the context of the "what is life?" discussion is that between complex systems and simple mechanisms. Clearly, being real systems, organisms are complex and therefore differ from machines. But that is too easy and of little value. There is more which can be done in answering the question that will make the answer rest on the living nature of the organism. To deal with this issue, Rosen developed a class of objects he named Metabolism-Repair systems, or more simply (M,R) systems. What he was able to do with these systems was to explore the answer to the question when well posed in terms of a prototypical organism. The idea was a category theory application to the dynamics of biochemical and physiological systems. The mapping described above can be seen as a generalization of the more simple input/output diagrams used by engineers and others, such as pharmacologists doing compartmental analysis. They also substitute nicely for chemical reaction kinetics. He called them abstract block diagrams. 

It is easy to model machines in terms of abstract block diagrams. The following is an example (Arbib and Manes, 1975). Let us look at a category theory formulation of a machine. It is surprisingly simple. It embodies everything a finiteTuring machine can do in an abstract way in terms of mappings. It also very nicely shows where dynamics comes into the entire picture. We next describe a sequential machine that can be in one of a finite number of states, receive one of a finite number of inputs, and emit one of a finite number of outputs.

Where

X₀ is the set of inputs

Q is the set of states

Y is the set of outputs

It has been said that this algorithmic character is restricted to sequential machines. I now will show that this is an illusion. A machine is a machine. Now can we describe a "parallel machine" as anything different?

Where

X₀ is the set of inputs

Q is the set of states

Y is the set of outputs

What is of particular interest is the mapping representing the dynamics of the machine. Even if we allow final cause into the picture, there is a paucity of entailment in the system. This will always be true in machines. In fact, if we try to answer "why?" for each aspect of the machine we can only finally answer by going outside the machine. This route leads to an infinite regression if continued. It is interesting that one way to end the process of nested entailments is to invoke some notion of deity.

The History of relational models goes back to a seminal paper by Nicholas Rashevsky wherein he made a radical change in his approach to living systems (Rashevsky, 1954). After pioneering most of the mechanistic models we know about today, including reaction-diffusion systems and artificial neural networks as far back as the 1930s, he took stock of what he had learned and realized that he was not any closer to understanding what living systems were all about. He then decided to take an entirely new direction. His goal was to keep the organization of the living system while basically throwing out the physics. His tool for this was topology.

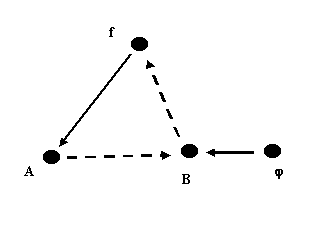
The broken lined arrows represent material causation and the solid arrows represent efficient cause. If we note that f has the meaning H (A,B) , namely some relation on the Cartesian product of sets A and B,

this can also be written as :

(A relation as used here is merely a subset of all the possible (A, B) with A coming from set a and B coming from set B.)

This idea of self-replication of functional components (not parts) of the system is the key to the resolution of the problem. It is important to fully understand this distinction. Function is distinct from structure. In complex systems function is "spread" over the parts of the system in a manner which does not map 1:1 onto those parts. To capture this essential property, Rosen utilized the functional component to represent this newly recognized reality within the system. The functional components are the ontological embodiment of the non-fragmentable aspects of the system's organization. They are defined by their context and have no necessary meaning outside that context. Thus, they capture what is lost by reductionism. The idea that functional components have the same reality as the parts, if not more, is very profound.

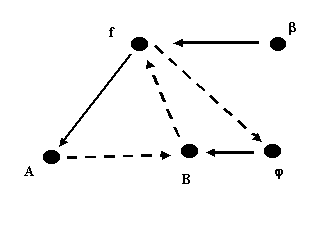
ß is left unentailed this time.

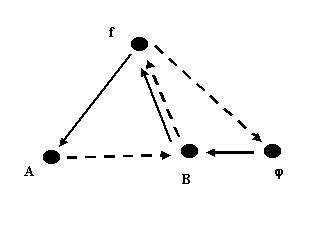
The diagram is one in which every function is entailed by another function. Thus the infinite regress seen in the machine does not exist and the question has been answered. Organisms are different from machines because they are closed to efficient cause. As Robert Rosen stated it "A material system is an organism if, and only if, it is closed to efficient causation. There is much that has been said in coming to this point and it is well worth summarizing.

The closure of the relational diagram has a parallel significance with Newton's achievement of closure in his dynamics. It establishes a category of objects called organisms that are clearly distinguishable from machines. This distinction arose from a procedure, which did not reduce the system to its material parts, nor did it explicitly invoke dynamics. In fact, the procedure, by necessity, treated processes and organization (mappings) as if they had the same ontological reality as the material parts. Specifically, to recognize mappings in which the mappings f play the role of material cause is to acknowledge a broader meaning for the notion of "material". Also, the concept of "replication" here is new and broadens the meaning of that term as well. What is replicated is a functional component, not a material part as such. It is necessary to recognize that the system of interest was complex, but that complexity alone was not enough. Thus organisms are complex, but all complex things are not organisms. The nature of the organism is that it possesses the kind of unity Maturana and Varela invoke for their autopoietic systems ( Maturana and Varela, 1980). It would seem appropriate for this result to be incorporated in the discussion of autopoiesis.

It should be clear from this result that not only is it useful to recognize functional components as making up separate tangible aspects of the system, but that it is necessary to do so. Once this idea becomes clear, it becomes possible to look at complex systems in a new and meaningful way. Up until now, these ideas have been poorly understood and the suggestion that there are non-material aspects to the system as important , if not more important, as the material parts has often been looked upon as a form of mysticism. On the contrary, in order for science to be less mystical, these aspects need to be given more consideration.

The question "what is life?" will probably never really be answered in that form. The reason is inbuilt in epistemology. Such a question is inherently ill posed. Instead, we ask to distinguish life from not-life and, in particular, the machine. The answer that presents itself is one we have recognized in other forms for years. We teach the cell theory "Living cells arise from other living cells". Modern cloning experiments and other manipulations are built on this notion and it seems to work well. Why not assemble a cell from its parts? The first response is usually that it is too complicated. What Rosen showed is something else. The issue is not one of complication, but one of complexity. Fabrication of complex systems is an entirely different project from the fabrication of a machine. This has interesting implications when we contemplate the evolution of life.

1. Evolution of life is not the construction of a machine

In this age of molecular biology it is very tempting to see the mysteries of evolution of living organisms as the evolution of some very complicated synthetic process. In fact, that notion is probably counter productive. A machine needs a builder; it can not effect its own construction. Evolution is a process that defines itself as a system. This is the idea captured in the concept of "component systems" (Kampis, 1991) and other related ideas. Rosen has laid a nice foundation for this manner of thinking. As early as 1958 he began to imagine the way life has to come about. As time progressed, the answer he saw was revolutionary. The machine oriented thinking of the Newtonian paradigm was a distraction. The contemplation of mechanism after mechanism for the answer to the problem led nowhere. The reason is clear, living things are not like machines at all. Machines are built from the bottom up out of parts constructed to add to each other in a supportive way. It is tempting to look at a machine and glibly say that the whole is more than the sum of the parts and think one has said something. Rosen simply asked, what is a sum of parts? This led to the modeling relation, the identification of some formalism that would define that sum, and the recognition that in every speculation about these matters models are involved. He then knew he had to understand those models. This led to a clear definition of what a machine is and how a machine relates to its parts. Once that was accomplished, it became obvious that living systems relate to their parts in entirely different ways. Evolution, as does the mature organism, must be seen as the evolution of function in the form of functional components. What is more, the functional components, because they are defined by the momentary context, are not permanent features in an evolving system. To the extent that a developing system mimics its evolution the same is true for it. How can this be realized? Rosen saw it in the abstract. He saw metabolism, repair, and replication. And there it is! The key to a system evolving to become an organism is that it must reach some point where it achieves all three of these functions. We have never designed a machine like this and for very good reason. We build machines to last. One of the first and most crucial aspects of the evolving living system was its failure to last! It was in a condition of being torn down as fast as it was being built up and this is what allowed it to evolve. Stability is the return to a condition after being perturbed from it. How much more stable could something be than to have both its construction and destruction under strict limits? Both construction and destruction are systems properties. The systematic tearing down allows rebuilding, replication and evolution. The details we know, but the strategy was masked by the details. Molecular biology is indeed an oxymoron. Biology is the study of life and life does not exist at the molecular level. We do not know how far Rosen went down this path. In a radio interview he speaks of unpublished work and some moral reservations about the responsibility he felt if he were to lead us further. It is clear from that strong conviction that, in his own mind, he saw an answer.

Science itself is a complex, evolving system. John Horgan, among others, has contemplated its end (Horgan, 1996). Interestingly, as he does that, he also mocks the many definitions of "complexity" and also only briefly mentions Robert Rosen as some "Canadian scientist", never mentioning his contributions to the topic he presents himself as expert in. On the other hand, Rosen wrote optimistically about the future of science (Rosen, 1996). His optimism was based on a direction for science that Horgan and many others rule out. Their bias is based on a strict adherence to a science of method rather than a science of content. Rosen saw that a science of content had its boundaries beyond our sight due to the newness of the ideas that sharpened his vision. There is more to life than that which a science of method allows access to. Human experience tells us that quite clearly. Rosen, with great skill, developed his tools from within the science of method. He used them to expose the limits and then break them down.

There is a lot being said in other circles about science and its role in the quest for knowledge in the future. For example, one brand of postmodern thought (Lyotard, 1979) recognizes an ongoing conflict between science and narrative as ways of knowing. These different realms may be in the process of becoming more complimentary as the development of these new ideas progresses. It is interesting that some writers have their feet planted in both arenas as they forge ahead (Hayles, 1995).

Rosen was ahead of his time when seen from that perspective. His work is difficult to master because it asks the learner to change directions. Often unlearning and relearning is necessary. It is easy to look at the above diagrams and dismiss them without understanding the immense semantic richness they carry with them. The ability to make that change makes it easy to continue to change. Is that not what evolution is all about? 

Arbib, M. and E. G. Manes. 1975. Arrows, Structures, and Functors: The Categorical Imperative. New York: Academic Press. pp 93-106.

Dress, W. 1998. "A Bayesian approach to extracting meaning from system behavior

1998 IEEE International Conference on Systems, Man, and Cybernetics. IEEE Press, pp. 2243-48.

Dress, W. 1999. Epistemology and Rosen's Modeling Relation. This Publication.

Fischler, M. A. and O. Firschein. 1987. Intelligence: The eye, the brain, and the computer. Reading:Addison Wesley.

Hayles, N. K. 1995. "Narratives of evolution and the evolution of narratives". in Cooperation and Conflict in General evolutionary processes. (J. L. Casti and A. Karlqvist, eds.). New York: Wiley. pp113-132.

Horgan, J. 1996. The end of science:facing the limits of science in the twilight of the scientific age. New York: Broadway Books.

Kampis, G. 1991. Self-Modifying Systems in Biology and Cognitive Science: A New Framework for Dynamics, Information and Complexity. New York: Pergamon Press.

Lovelock, J. 1979. Gaia: A new look at life on earth. Oxford: Oxford University Press.

Lyotard, J.-F. 1979. The postmodern condition: A report on knowledge.Minneapolis: The University of Minnesota Press.

Maturana, H. R. and F. J. Varela. 1980. Autopoieses and cognition: The realization of the living. Dordrecht: D. Reidel.

Mikulecky, D. C. 1993. Applications of network thermodynamics to problems in biomedical engineering. New York: New York University Press.

Mikulecky, D. C. 1994."n-ports: what are they good for?" Special Issue: Modeling Complex Biological Systems, Math. And Comp. Modeling. Vol. 19: 99-118.

Mikulecky, D. C. and M. Thellier. 1993. "Determining transient kinetic behavior of complex multi-enzyme systems by use of network thermodynamics. C. R. Acad. Sci. III. Vol. 316(12): 1399-1403.

Peusner, L. 1970. The principles of network thermodynamics: theory and biophysical applications. Ph. D. Thesis. Harvard University. (reprinted by Entropy Limited, Lincoln, MA, 1987)

Peusner, L. 1986. Studies in network thermodynamics. Amsterdam: Elsevier.

Prideaux, J. 1996. "Feed-forward activation in a theoretical first-order biochemical pathway which contains an anticipatory model. Acta Biotheoretica. Vol. 44:219-233.

Rashevsky, N.1954. "Topology and life: In search of general mathematical principles in biology and sociology". Bull.Math. Biophys. Vol.16: 317-348.

Rosen, R., Some relational cell models: The metabolism-repair systems, in Foundations of Mathematical Biology, Volume II, R. Rosen, ed. Academic Press, NY, 1972.

Rosen, R. 1978. Fundamentals of Measurement and representation of Natural Systems. New York :North-Holland

Rosen, R. 1985.Anticipatory Systems: Philosophical, Mathematical & Methodological

Foundations, New York: Pergamon Press.

Rosen, R. 1991.Life Itself: A Comprehensive Inquiry into the Nature, Origin, and Fabrication of

Life. New York: Columbia University Press.

Rosen, R. 1996. "On the limits of Scientific knowledge" in Boundaries and barriers:on the limits to scientific knowledge. (J. L. Casti and A. Karlqvist, eds.). Reading: Addison-Wesley. pp199-214.