
|
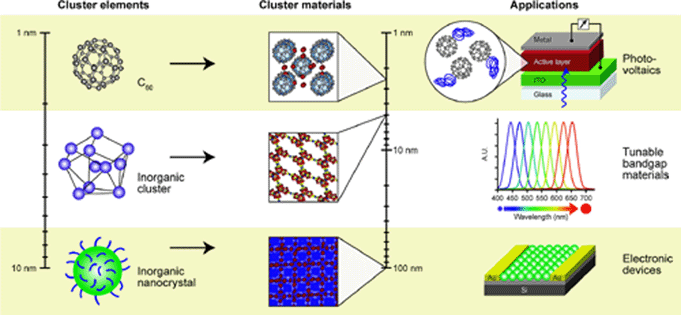
Cluster
Assembled Materials
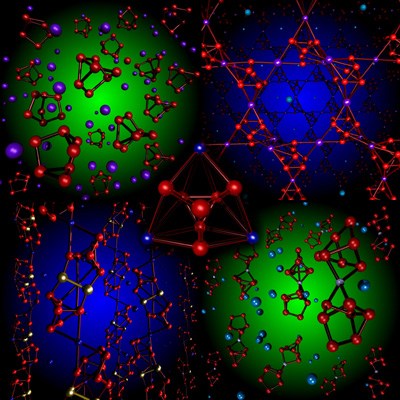 Cluster
assembled materials are solids in which clusters serve
as the building
blocks. These materials allow
the integration of multiple length scales into a hierarchical
material. Since the properties of clusters change with
size,
composition, and oxidation state, and the emergent
behaviors
depend on the their architecture, cluster assemblies form
materials with tunable properties. These materials serve
as
links between the
predictable size-invariant properties of solids and the
evolution in
properties observed at the subnanometer scale where every atom
and every electron count. The materials retain many of the
characteristics of the original
building blocks. Cluster motifs
coupled by linkers offer unusual properties because they combine
intra-cluster, inter-cluster, and linker-cluster interactions,
unavailable in atomic solids. The fundamental
question is,
what controls the properties once the clusters are incorporated
into an
extended nanoscale material? Cluster
assembled materials are solids in which clusters serve
as the building
blocks. These materials allow
the integration of multiple length scales into a hierarchical
material. Since the properties of clusters change with
size,
composition, and oxidation state, and the emergent
behaviors
depend on the their architecture, cluster assemblies form
materials with tunable properties. These materials serve
as
links between the
predictable size-invariant properties of solids and the
evolution in
properties observed at the subnanometer scale where every atom
and every electron count. The materials retain many of the
characteristics of the original
building blocks. Cluster motifs
coupled by linkers offer unusual properties because they combine
intra-cluster, inter-cluster, and linker-cluster interactions,
unavailable in atomic solids. The fundamental
question is,
what controls the properties once the clusters are incorporated
into an
extended nanoscale material?
Cluster-assembled materials combine the nanoscale size and
composition-dependent properties of clusters and embed them in
potentially functional materials. To understand the
emergent
properties as the clusters are assembled into hierarchical
materials,
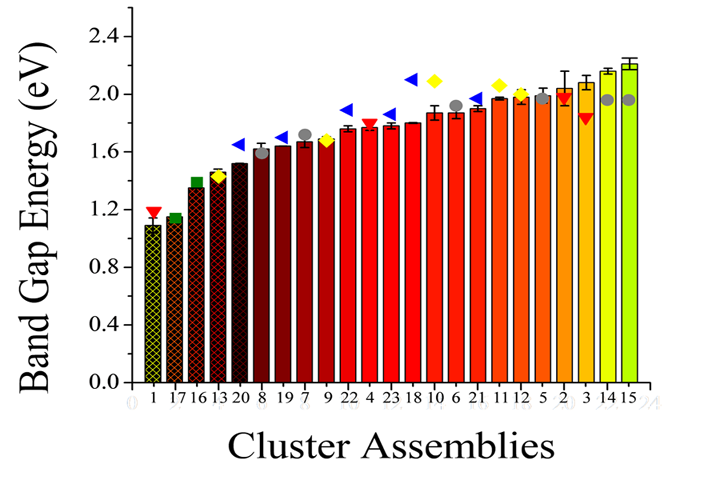
we have synthesized 23 cluster-assembled materials composed of
As73--based motifs and
different countercations, and measured their
band gap energies. The results reveal that the band gap
energy
can be varied from 1.09 eV to 2.21 eV. First principles
electronic
structure studies have been carried out to identify the physical
mechanisms, which enable control of the band gap edges of the
cluster
assemblies.
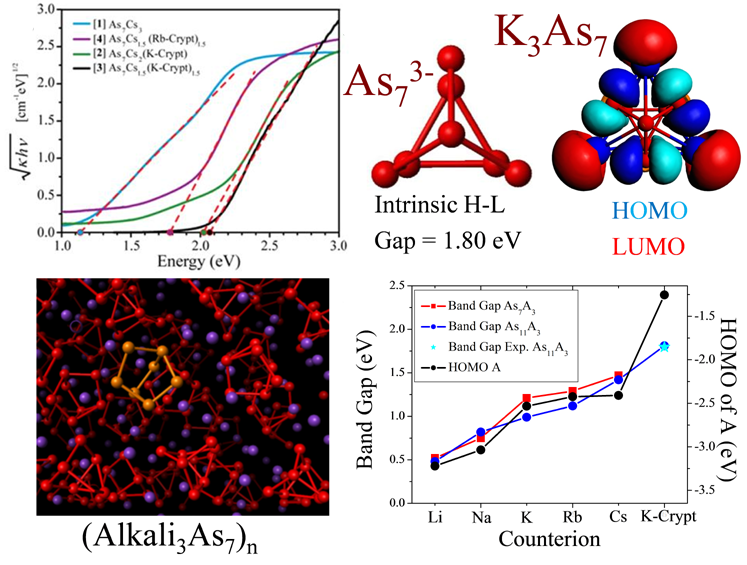
To
probe
the origins of the variation in the band gap energies, we
examined the nature of the frontier orbitals in isolated A3As7
clusters. The HOMO and LUMO charge densities are plotted
below. The HOMO is composed of contributions from the As
atoms, and the LUMO is localized on the alkali metal
cations.
Further, the LUMO of the material is derived from the
absolute position of the HOMO of the neutral alkali metal
atom.
This close correlation is seen below, which shows the energies of
the
HOMOs of the alkali metal atoms and the calculated band gap energy
of
the pure Zintl materials. These were obtained by calculating
the
band structures of optimized A3As7
and A3As11 assemblies for
various alkali atoms in the observed orthorhombic and monoclinic
structures of Cs3As7 and
Cs3As11. The
experimental and theoretical band gap energy for [K-Crypt]3[As11]
are also included. The HOMO of the free neutral atom is
lowest
for lithium and increases as the size of the atom increases,
except for
the cryptated potassium, in which the lone pair on the polyether
greatly destabilizes the HOMO. Mixing of the states is
evident in
solids containing multiple countercations, as replacing a single
Cs
atom with cryptated K ions results in an increase of Ebg from 1.1
to
2.1 eV. The nature of the countercation is the dominant
factor to
controls the band gap energy in these assemblies.
 The HOMO-LUMO gap of the isolated [As7]3-
cluster is 1.80 eV, however the band gap energy of the 2D sheets
of [As7]3-
linked by Cs and Rb and separated by K-Crypt are consistently
larger
ranging from 1.97 to 2.08 eV. Changing the assembly from a
0D
to
a 2D architecture is generally expected to decrease the band gap
energy
through increased band broadening due to larger coordination,
however
we observe an increase in band gap energy.30 To understand
this
phenomenon, we extended our search to the [Au2(As7)2]4-
composite cluster in which we synthesized multiple counterion
directed
architectures of have the same basic building [As7Au2As7]4-,
but changing the cation results in 0D and 2D
architectures.
The experimental band gap energy of the 0D compound is found to
be 1.69
eV and is in good agreement with the theoretically calculated
value of
1.68 eV. We also synthesized structures that are 2D layers
formed
by interactions of Rb and Cs cations with [Au2(As7)2]4-,
while cryptated alkali cations separate these layers. The
band
gap energies of the 2D compounds are found to be 1.87, 1.97, and
1.98
eV, respectively, and are in good agreement with the
theoretically
calculated values. The band gap energies for all of the 2D
assemblies are larger than the band gap energy of the 0D
assembly,
whose band gap energy is expected to be the upper limit.
The HOMO-LUMO gap of the isolated [As7]3-
cluster is 1.80 eV, however the band gap energy of the 2D sheets
of [As7]3-
linked by Cs and Rb and separated by K-Crypt are consistently
larger
ranging from 1.97 to 2.08 eV. Changing the assembly from a
0D
to
a 2D architecture is generally expected to decrease the band gap
energy
through increased band broadening due to larger coordination,
however
we observe an increase in band gap energy.30 To understand
this
phenomenon, we extended our search to the [Au2(As7)2]4-
composite cluster in which we synthesized multiple counterion
directed
architectures of have the same basic building [As7Au2As7]4-,
but changing the cation results in 0D and 2D
architectures.
The experimental band gap energy of the 0D compound is found to
be 1.69
eV and is in good agreement with the theoretically calculated
value of
1.68 eV. We also synthesized structures that are 2D layers
formed
by interactions of Rb and Cs cations with [Au2(As7)2]4-,
while cryptated alkali cations separate these layers. The
band
gap energies of the 2D compounds are found to be 1.87, 1.97, and
1.98
eV, respectively, and are in good agreement with the
theoretically
calculated values. The band gap energies for all of the 2D
assemblies are larger than the band gap energy of the 0D
assembly,
whose band gap energy is expected to be the upper limit.
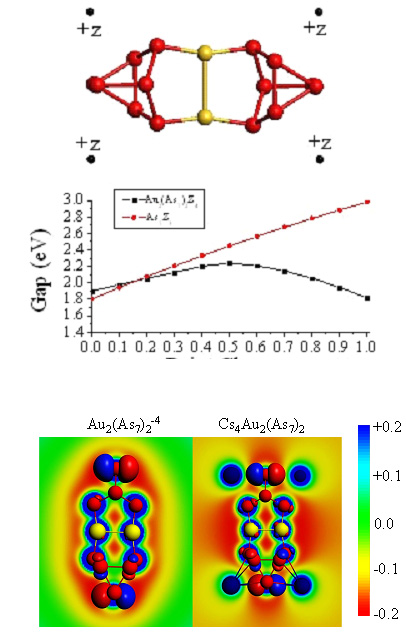
How
does varying the architecture of the assembly increase the band
gap
energy to a larger value than that of an isolated cluster
motif?
Our
hypothesis is that the counterions connected to the clusters
generate an internal electric field that alters the band gap
energy
through modulating orbitals at the band edge in a manner
analogous to
crystal field theory. To demonstrate this, we calculated
the
electronic structure for an isolated [Au2(As7)2]4-
cluster with four point charges, z, placed at the same positions
as Cs
in the solid. The point charges were varied from 0.0 to
+1.0e,
and the HOMO-LUMO gap and electronic spectrum was
monitored.
The
HOMO-LUMO gaps increased by 0.34 eV when varying the point
charge from
0 to +0.5e for the gold-linked clusters and then to decrease
with
higher fields. We found that the increase in the HOMO-LUMO
gap is
caused by stabilization of the HOMO with increasing field, while
the
LUMO states show little change until z = +0.6e. Further,
increased electric fields reduce the gap as the As-Au mixed
states are
strongly stabilized to become the LUMO at high field.
Similar
electric-field-dependent behavior is observed for [As7]3-
clusters, however the gap increases monotonically up to 2.98 eV
with
increasing electric field (Figure 5b). We confirmed this
by
examining the local electrostatic environment of our cluster
models in
Figure 5c with the associated HOMO plotted as an
isosurface.
Figure 5c shows the electrostatic potential of [(Au2)(As7)2]4-
and Cs4[(Au2)(As7)2]
as the electric field corresponds to the gradient of the
electrostatic
potential; a red to blue sequence indicates a stronger electric
field. In [(Au2)(As7)2]4-,
the electrostatic potential falls off gradually from the
isolated
cluster because no adjacent counterions are present to generate
internal electric fields. In contrast, for the case of Cs4[(Au2)(As7)2],
there
is a large electric field generated by the Cs counterions,
precisely along the path of the HOMO orbital. The band gap
energy
variation also depends on the precise location of the electric
field
generated by the counterion and by the charge density of the
states
near the Fermi energy, so it may not always result in an
increase of
the band gap energy. These results show that the band gap
energies of the 2D ionic solids increase due to the generation
of
internal electric fields by the adjacent counterions.
References:
Cluster
Assembled Materials
1) Palladium
in the Gap: Cluster
Assemblies with Band Edges Localized on Linkers.
A.C. Reber, S. Mandal, M. Qian, H.M. Saavedra, P.S. Weiss,
S.N. Khanna,
A. Sen. J. Phys. Chem. C 116, 10207-10214 (2012).
2) Synthesis,
structure, and band
gap energy of covalently linked cluster-assembled
materials.
S.
Mandal, A.C. Reber, M. Qian, R.Liu, H.M. Saavedra, S.Sen,
P.S.
Weiss, S.N. Khanna, A. Sen. Dalton Trans. 41,
12365-12377
(2012).
3) On
the stability of an
unsupported mercury-mercury bond linking group 15 Zintl
clusters.
S.
Mandal, A.C. Reber, M. Qian, R. Liu, H.M. Saavedra, S.
Sen, P.S. Weiss,
S.N. Khanna, A. Sen. Dalton Transactions. 41, 5454-5457
(2012).
4) [As7M(CO)3]3-
M=Cr,Mo,W:
Bonding and Electronic Structure of Cluster assemblies
with Metal
Carbonyls
S. Mandal, M. Qian, A.C. Reber, H.M. Saavedra, P.S. Weiss,
S.N. Khanna,
A. Sen. J Phys. Chem. C 115, 20217 (2011).
5)
The Zintl ion [As7]2-: an
example of electron deficient Asx radical anion. S.
Mandal, R. Liu, A.C. Reber, M. Qian, H.M. Saavedra, X. Ke,
P. Schiffer,
S. Sen, P.S. Weiss, S.N. Khanna, A. Sen. Chem.
Commun. 47,
3126
(2011).
6) Controlling
Band gap Energies
in Cluster-Assembled Ionic Solids through Internal
Electric Fields.
N.K.Chaki, S. Mandal, A.C. Reber, M. Qian, H.M. Saavedra,
P.S. Weiss,
S.N. Khanna, and A. Sen. ACS Nano 4, 5813
(2010).
7) Cluster-Assembled
Materials:
Toward Nanomaterials with Precise Control over Properties.
M. Qian, A.C. Reber, A. Ugrinov, N.K. Chaki S. Mandal,
H.M. Saavedra,
S.N. Khanna, A. Sen and P.S. Weiss. ACS Nano 4 235 (2010).
8) Helical
and
linear [K(As11)]2- chains: Role of solvent on the
conformation of
chains formed by Zintl anions. A.C. Reber, A.
Ugrinov, A.
Sen, M.
Qian, and S.N. Khanna. Chem Phys. Lett. 473 305 (2009).
9) [Te2As2]-2
:
A Planar Motif with "Conflicting" Aromaticity. A.
Ugrinov,
A.
Sen, A.C. Reber, M. Qian, and S.N. Khanna. J. Amer. Chem.
Soc. 130, 782
(2008).
10)
From Designer Clusters to Synthetic Crystalline
Nanoassemblies.
A.W. Castleman Jr., S.N. Khanna, A. Sen, A.C. Reber,
M. Qian,
K.M. Davis, S.J. Peppernick, A. Ugrinov, and M.D. Meritt.
Nano Letters
7 2734 (2007).
11) Cluster
Assembled Materials"
S.A.
Claridge, A.W. Castleman Jr., S.N.
Khanna, C.B. Murray, A. Sen, P.S. Weiss. ACS
Nano 3 244 (2009).
12) Superatom
Compounds,
Clusters, and Assemblies: Ultra
Alkali Motifs and Architectures. A.C.
Reber, S.N. Khanna, and A.W.
Castleman Jr. J. Amer.
Chem Soc. 129 10189 (2007).
|
|


