Linear Algebra
Test #2
May  5, 2003
Name____________________
R.  Hammack
Score ______


(1) This problem concerns the matrix A = (1 2 2 1) 1 1 1 1 1 0 1 1.
(a) Is (1 ) -1 -1 1 in the null space of A?



(b) Is [2  9  7  2]  in the row space of A?

 



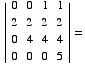
(2)    | 0 0 1 1 | = 2 2 2 2 0 4 4 4 0 0 0 5   
(3) Find the inverse of this matrix without doing any row reductions. (Hint: is it orthogonal?) (1 1 1 ) - -- ------- 2 2 ... 1 - - ------- 2 2 0 Sqrt[2]



(4) Suppose W = { (x) | 3 x - 2 y + 7 z = 0 } y z.   Find W^⊥.

 

 

(5) Consider the matrix A = (-1 1 0 ) 0 1 0 0 1 -1
(a) Find the eigenvalues of A.

 




(b) Find the eigenspaces of A.


 




(c) Diagonalize the matrix A, that is find an invertible matrix P and a diagonal matrix D with P^(-1) A P = D.

 



(6) Suppose !, = {u _ 1, u _ 2, u _ 3}is an orthogonal basis for ÷µ^3having the property that || u _ 1 || = 1, || u _ 2 || = 2, and || u _ 3 || = 3. Suppose also that v ∈ ÷µ^3satisfies v · u _ 1 = 2,  v · u _ 2 = 5, and  v · u _ 3 = 6. Find [v] _ !,.

 




(7) Suppose !, = {u _ 1, u _ 2, u _ 3}is a basis for ÷µ^3,  and  T : ÷µ^3 -> ÷µ^2 is a linear transformation for which T(u _ 1) = (3) 0,  T(u _ 2) = (1) 1, and T(u _ 3) = (0 ) -1. Moreover, suppose v is a vector in  ÷µ^3for which  FormBox[RowBox[{v, =, Cell[TextData[{3, Cell[BoxData[u ]], +2, Cell[BoxData[u ]], +5, Cell[Box ... 1 2 3.  Find T(v).

 




(8) Suppose A is a matrix which has 5 rows, and the rows are linearly independent. Suppose also that Null(A) is two-dimensional. How many columns does A have?

 




(9) Suppose A is a 5×5 matrix with a one-dimensional null space.   Find det(A).