Calculus I Diagnostic Quiz February 9, 2004
Name____________________ R. Hammack Score ______
_______________________________________________________________________
(1) Find all solutions:
Solutions: x = 2 and x = -2
(2) Find all solutions:
It's a quadratic set equal to 0 and it doesn't factor,
so we use the quadratic formula:
Solutions:
Thus, there are two solutions:
(3) Find all solutions:
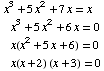
Solutions: x=0, x= -2 and x= -3
(4)
(5) Simplify as much as possible:
(6) A straight line has slope 2 and x-intercept 3. What is its y-intercept?
Call the y-intercept b.
The equation of the line is y=2x+b.
The x-intercept being 3 means y = 0 when x=3.
Plug this in and the equation becomes: 0=2(3)+b, or 0=6+b.
From this, the y-intercept is