_____________________________________________________________________________________
Calculus I                                                                      Test #3                                             December 1, 2004

Name____________________                               R.  Hammack                                             Score ______
_____________________________________________________________________________________

(1) Find the inverse of the function f(x) = 5 + e^(3x + 2)
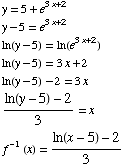
y = 5 + e^(3x + 2)  y - 5 = e^(3x + 2)  ln(y - 5) = ln(e^(3x + 2))  ln ... #62371; ln(y - 5) - 2 = 3x  (ln(y - 5) - 2)/3 = x  f^(-1) (x) = (ln(x - 5) - 2)/3


(2)  Is the function g(x) = 5x + 3e^x  invertible or not?  Explain.

Since g ' (x) = 5 + e^xis positive for all x,  the function g(x) increases and never decreases.
Hence it passes the Horizontal Line Test, so it's invertible.


(3) Find the equation of the tangent line to the graph of  y = sin^(-1)(x) at the point where x = 3^(1/2)/2.

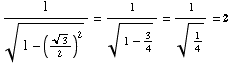
Slope at x is y ' =1/(1 - x^2)^(1/2). Thus the slope of the tangent is 1/(1 - (3^(1/2)/2)^2)^(1/2) = 1/(1 - 3/4)^(1/2) = 1/1/4^(1/2) = 2

Point of tangency is (3^(1/2)/2, sin^(-1)(3^(1/2)/2)) = (3^(1/2)/2, π/3)

Point-Slope formula: y - π/3 = 2 (x - 3^(1/2)/2)

ANSWER:  y = 2x - 3^(1/2) + π/3


(4)  Solve the equation  5^(x - 1) = 3e^x.

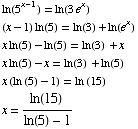
ln(5^(x - 1)) = ln(3e^x)  (x - 1) ln(5) = ln(3) + ln(e^x)  x ln(5) - ln(5) = l ... ; x ln(5) - x = ln(3) + ln(5)  x (ln (5) - 1) = ln (15)  x = ln(15) /(ln(5) - 1)


(5) Simplify each expression as much as possible.

(a)  FormBox[RowBox[{RowBox[{81, ^, RowBox[{(, RowBox[{-, 0.75}], )}]}], =}], TraditionalForm]FormBox[RowBox[{StyleBox[RowBox[{1, /, RowBox[{81, ^, 0.75}]}], FontSize -> 14], =, 1/81^(3/4) = 1/81^(1/4)^3 = 1/3^3 = 1/27}], TraditionalForm]

(b)  cos^(-1)(-1/2) =(2π)/3

(c)  ln ( 1 ) = 0

(d)  4^(2log_4(5)) =4^log_4(5^2) = 25

(e)  sec^(-1) ( ln(e^3e^(-1)) ) =sec^(-1) ( ln(e^(3 - 1)) ) = sec^(-1) ( ln(e^2) ) = sec^(-1)(2) = π/3

(6)   The graph of the derivative of a function f is given. [Graphics:HTMLFiles/index_23.gif]
In each case, indicate whether the ? should be replaced with the symbol <, >,  or =.

(a)      f(1)   ?     f(3)  ANSWER: > , because f decreases between 1 and 3 (its derivative is negative there).

(b)    f '(1)   ?    f '(3)  ANSWER: =, by reading straight from the graph.

(c)    f "(1)   ?    f "(3)  ANSWER: <, by looking at slope on the graph of f '

(7) Find the derivatives.

(a)   d/dx[ 6^x ] =ln(6) 6^x

(b) d/dx[log(x)] = 1/(ln(10) x)

(c) d/dx[ ln(x)] = 1/x

(d)  d/dx[ e^(4x + ln(x))] = e^(4x + ln(x))(4 + 1/x)

(e) d/dx[ tan^(-1)(x) ln(tan(x))] =1/(1 + x^2) ln(tan(x)) + tan^(-1)(x) sec^2(x)/tan(x)

(f) d/dx[ln(x)/e^x] = (1/xe^x - ln(x) e^x)/(e^x)^2 = e^x (1/x - ln(x))/(e^x)^2 = (1/x - ln(x))/e^x

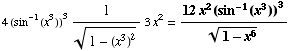
(g)  d/dx[ (sin^(-1)(x^3))^4 ] =4 (sin^(-1)(x^3))^31/(1 - (x^3)^2)^(1/2) 3x^2 = (12x^2(sin^(-1)(x^3))^3)/(1 - x^6)^(1/2)

(h) d/dx[  x^x] = x^x (ln(x) + 1), using logarithmic differentiation, as below.

y = x^x  ln(y) = ln(x^x)  ln(y) = x ln(x)  d/dx[ln(y)] = d/dx[x ln(x)]  1/yy ' = ln(x) + x1/x  y ' = y (ln(x) + 1)  y ' = x^x (ln(x) + 1)


(8)  Consider the function f(x) = x^4 + 8x^3 + 18x^2 - 8.

(a)    List all critical points of f.

f ' (x) = 4x^3 + 24x^2 + 36x = 4x(x^2 + 6x + 9) = 4x(x + 3)^2
From this you can read off the critical points as 0 and -3

(b)     Find the intervals on which f increases/decreases.
   -3      0
---|------|-----
- - - - - - + + +f '(x)

f increases between 0 and infinity.
f decreases between negative infinity and 0

(c)     Find the intervals on which f  is concave up/down.

f '' (x) = 12x^2 + 48x + 36 = 12 (x^2 + 4x + 3) = 12 (x + 1) (x + 3)

   -3      -1
---|------|-----
++ - - -  + + +f ''(x)

f is concave down on [-3,-1]
Elsewhere, f is concave up

(d)    Locate and identify all extrema of f .

By first derivative test (see part b above) there is a relative minimum at x = 0.
There is no relative maximum.

(e)    List the locations (x-values) of all inflection points of f.

By part c above, the locations are -3 and -1.