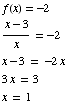_______________________________________________________________
Calculus I Test
#1 October 5,
2004
Name _________________ R.
Hammack Score______
Directions. Answer in the space provided. Show as much work as is reasonable.
_______________________________________________________________
(1)
(a) 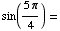
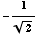
(b) 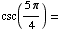
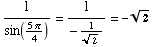
(c) Suppose 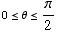 , and
, and
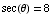 . Find
. Find
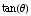 .
.
From sec(θ)=8, we get 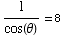 ,
or
,
or 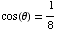 .
.
Also, 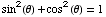 ,
meaning
,
meaning 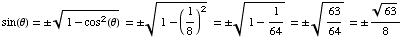
Then 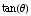 =
=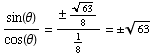 . But,
as
. But,
as 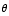 is in the first quadrant,
is in the first quadrant, 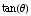 is the POSITIVE square root of 63.
is the POSITIVE square root of 63.
(d) Find all
solutions of the equation 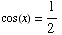
![[Graphics:HTMLFiles/T1F04A_16.gif]](HTMLFiles/T1F04A_16.gif)
Looking at the unit circle, you can see that the solutions are all values of
x of the form
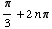 or
or 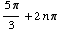 ,
where n is an integer.
,
where n is an integer.
(2) Suppose 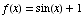 and
and 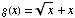 .
.
(a) 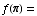 sin(
sin(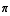 )+1
= 1
)+1
= 1
(b) 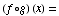
![FormBox[RowBox[{f(g(x)), =, RowBox[{sin(x^(1/2) + x), +, RowBox[{1, Cell[]}]}]}], TraditionalForm]](HTMLFiles/T1F04A_24.gif)
(c) 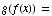
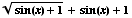
(d) 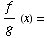
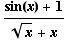
(e) State the domain
of f. All
real numbers.
(f) State the range
of f. [0,
1]
(3) Find the equation of the line having
slope 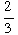 and passing through (4, 5). Put your answer in slope-intercept form.
and passing through (4, 5). Put your answer in slope-intercept form.
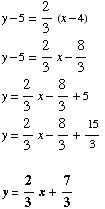
(4) ![Underscript[lim , x1] (x^3 - 3x + 1) =](HTMLFiles/T1F04A_31.gif)
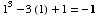
(5) ![Underscript[lim , x1] (x - 1)/(x^4 - x^3) =](HTMLFiles/T1F04A_33.gif)
![Underscript[lim , x1] (x - 1)/x^3(x - 1) = Underscript[lim , x1] ( 1)/x^3 = 1](HTMLFiles/T1F04A_34.gif)
(6) ![Underscript[lim , x16] (x ^(1/2) - 4)/(x - 16) =](HTMLFiles/T1F04A_35.gif)
![Underscript[lim , x16] (x ^(1/2) - 4)/(x - 16) (x ^(1/2) + 4)/(x ^(1/2) + 4) = Undersc ... - 16) (x ^(1/2) + 4)) = Underscript[lim , x16] 1/(x ^(1/2) + 4) = 1/(16 ^(1/2) + 4) = 1/8](HTMLFiles/T1F04A_36.gif)
(7) ![Underscript[lim , x3] (1/3 - 1/( x))/(x - 3) =](HTMLFiles/T1F04A_37.gif)
![Underscript[lim , x3] (x - 3)/(3x) /(x - 3) = Underscript[lim , x3] (x - 3)/(3 ... lim , x3] (x - 3)/(3x) 1/(x - 3) = Underscript[lim , x3] 1/(3x) = 1/(3 (3)) = 1/9](HTMLFiles/T1F04A_38.gif)
(8) ![Underscript[lim , x3] (x^2 - 9)/(x - 3) =](HTMLFiles/T1F04A_39.gif)
![Underscript[lim , x3] ((x + 3) (x - 3))/(x - 3) = Underscript[lim , x3] (x + 3) = 3 + 3 = 6](HTMLFiles/T1F04A_40.gif)
(9) ![Underscript[lim , x∞] (2x + 1)/(3x^2 + 1)^(1/2) =](HTMLFiles/T1F04A_41.gif)
![Underscript[lim , x∞] (2x + 1)/(3x^2 + 1)^(1/2) (1/x)/(1/x) =](HTMLFiles/T1F04A_42.gif)
![Underscript[lim , x∞] (2 + 1/x)/((3x^2 + 1) (1/x)^2)^(1/2) = Underscript[lim , x∞] (2 + 1/x)/(3 + 1/x^2)^(1/2) = (2 + 0)/(3 + 0)^(1/2) = 2 /3^(1/2)](HTMLFiles/T1F04A_43.gif)
(10) ![Underscript[lim , x∞] (8 - x^3)/(x - 10) =](HTMLFiles/T1F04A_44.gif)
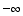
(11) ![Underscript[lim , x0^+] sin(x)/(5x^(1/2)) =](HTMLFiles/T1F04A_46.gif)
![Underscript[lim , x0^+] sin(x)/(5x^(1/2)) x^(1/2)/x^(1/2) = Underscript[lim , x0^+] sin(x)/(5x) x^(1/2) = 1/50^(1/2) = 0](HTMLFiles/T1F04A_47.gif)
(12) ![Underscript[lim , x0] cos(x + π) =](HTMLFiles/T1F04A_48.gif)
![cos(Underscript[lim , x0] (x + π)) = cos(π) = -1](HTMLFiles/T1F04A_49.gif)
(13) ![Underscript[lim , x0] (x sin(x) - x^3)/(4x^2) =](HTMLFiles/T1F04A_50.gif)
![Underscript[lim , x0] ((x sin(x))/(4x^2) - x^3/(4x^2)) = Underscript[lim , x0] (sin(x)/(4x) - x/4) = 1/4 - 0 = 1/4](HTMLFiles/T1F04A_51.gif)
(14) Consider the function
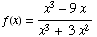 .
.
Note
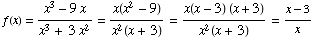 (provided x is neither 0 nor -3 )
(provided x is neither 0 nor -3 )
(a) At which values
of x is f discontinuous?
0 and -3 because f is not defined there
(b) Find the vertical asymptotes (if any) of f.
The denominator is 0 for x = 0, or -3. These are the candidates for the locations
of the vertical asymptotes.
![Underscript[lim , x -3^+] f(x) = Underscript[lim , x -3^+] (x - 3)/x = 2](HTMLFiles/T1F04A_54.gif) ,
so no asymptote here.
,
so no asymptote here.
![Underscript[lim , x0^+] f(x) = Underscript[lim , x0^+] (x - 3)/x = ∞](HTMLFiles/T1F04A_55.gif) ,
so line x=0 is a V.A.
,
so line x=0 is a V.A.
(c) Find the horizontal asymptotes (if any) of f.
![Underscript[lim , x∞] f(x) = Underscript[lim , x∞] (x^3 - 9x)/(x^3 + 3x^2) = 1](HTMLFiles/T1F04A_56.gif) ,
so line y = 1 is the horizontal asymptote.
,
so line y = 1 is the horizontal asymptote.
(d) For which values of x
does 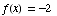 ?
?
We need to solve
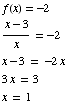
Answer: x = 1
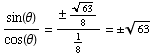 . But,
as
. But,
as ![[Graphics:HTMLFiles/T1F04A_16.gif]](HTMLFiles/T1F04A_16.gif)
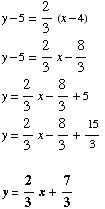
![Underscript[lim , x3] (x - 3)/(3x) /(x - 3) = Underscript[lim , x3] (x - 3)/(3 ... lim , x3] (x - 3)/(3x) 1/(x - 3) = Underscript[lim , x3] 1/(3x) = 1/(3 (3)) = 1/9](HTMLFiles/T1F04A_38.gif)
![Underscript[lim , x∞] (2 + 1/x)/((3x^2 + 1) (1/x)^2)^(1/2) = Underscript[lim , x∞] (2 + 1/x)/(3 + 1/x^2)^(1/2) = (2 + 0)/(3 + 0)^(1/2) = 2 /3^(1/2)](HTMLFiles/T1F04A_43.gif)