_____________________________________________________________
Calculus I                                         Quiz 3                       September 21, 2004

Name _________________        R. Hammack                              Score_____
_____________________________________________________________

(1) Find the equation of the line that passes through the point (5, 9) and has x-intercept 7.
Please express your answer in slope-intercept form.

We know 2 points on the line.  (5, 9) and (7, 0).  Thus its slope is

Using the point-slope form of the equation for a line, we get



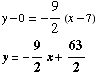
(2)
(a)    (by looking at the unit circle)


(b)    -1
(Because any radian measure that's an odd multiple of corresponds to the point (-1, 0) on the unit circle.)


(3)  Find all values of x (in radians) for which .

From the unit circle, you can see that if , then tan(x) = -1.


But note also you can add any integer multiple of to this value, and still  tan(x) = -1.

SOLUTION:  


(4)  Suppose x is a number for which .  What are the possible values for ?

From the identity , we get  , or  .
Thus ,    so  .

Now,