__________________________________________________________________
Calculus I                                               Quiz  #1                        September 10, 2004

Name____________________         R.  Hammack                            Score ______
_________________________________________________________________

 The problems on this quiz involve the functions  f(x) = (4 - x^2)^(1/2) and  g(x) = (3 - x)^(1/2).


(1)   Find the value(s) of x for which f(x) = g(x).

The answers to this question are the solutions of the equation
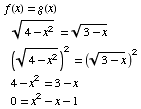
f(x) = g(x)  (4 - x^2)^(1/2) = (3 - x)^(1/2)  ((4 - x^2)^(1/2))^2 = ((3 - x)^(1/2))^24 - x^2 = 3 - x0 = x^2 - x - 1
Since this quadratic doesn't easily factor, we use the quadraitic formula.
x = (-(-1) ± ((-1)^2 - 4 (1) (-1))^(1/2))/2 = (1 ± 5^(1/2))/2
Thus (1 + 5^(1/2))/2and (1 - 5^(1/2))/2are the two values of x for which f(x) = g(x).


(2)   Find the domain of the function  f.   

f(x) = (4 - x^2)^(1/2)
Since we can't have a negaitve value inside the square root, we insist that
4 - x^2≥0  (2 + x) (2 - x) ≥0

      -2           2
----+--------+-----
- - -| + + + | + + + (2+x)
+ + | + + + | - - - - - (2-x)
- - - | + + + | - - - - - (2+x)(2-x)

Thus, you can see that the domain is the set [-2, 2].


(3)   Suppose   h(x) = {f(x)       if x> -2 g(x)        if x≤ -2


(a)  h(-5) =g(-5) = (3 - (-5))^(1/2) = 8^(1/2) = 22^(1/2)


(b)  h(1) =f(1) = (4 - 1^2)^(1/2) = 3^(1/2)