_____________________________________________________________________________
Calculus I Final
Exam December
13, 2001
Name____________________ R. Hammack Score
______
_____________________________________________________________________________
(1) Calculate the limits.
(a) ![Underscript[lim , x3]](HTMLFiles/ExF01_1.gif)
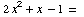
(b) ![Underscript[lim , x0]](HTMLFiles/ExF01_4.gif)
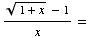
(c) ![Underscript[lim , x4]](HTMLFiles/ExF01_13.gif)
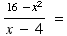
(2)
Find the derivatives of the following functions. You may use any applicable
rule. You do not need to simplify your answer.
(a)
f(x)
= 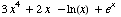 f
' (x)
=
f
' (x)
=
(b) f(x)
= 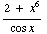 f
' (x)
=
f
' (x)
=
(c) y
= 
(d) ![d/dx[ tan^(-1)(2 + ln x) ] =](HTMLFiles/ExF01_25.gif)
(e) ![d/dx[x^2e^sec (x)] =](HTMLFiles/ExF01_28.gif)
----------------------------------------------------------------------------------------------------------------------
(3) The questions on this page concern
the function 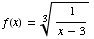
(a) ![Underscript[lim , x4] f(x) =](HTMLFiles/ExF01_31.gif)
(b) ![Underscript[lim , x∞] f(x) =](HTMLFiles/ExF01_33.gif)
(c) ![Underscript[lim , x3^+] f(x) =](HTMLFiles/ExF01_34.gif)
(d) State the horizontal asymptotes
of f.
(e) State the vertical asymptotes of
f.
(f) Find the inverse of f. (You
may assume that f is one-to-one.)
(g) Find the derivative of
f.
(h) Find the equation of the line tangent
to the graph of y = f(x)
at the point x = 2.
______________________________________________________________________________
(4) This problem concerns the function 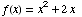 .
.
(a) 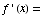
(b) Find all critical points of f.
(c) Find the absolute maximum and minimum
values of f on the interval [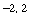 ].
].
(5) This problem concerns the function
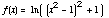 .
.
(a) 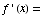
(b) Find all critical points of f.
(c) State the intervals on which f
is increasing and those on which it is decreasing.
(d) List the locations of all relative
maxima of f.
(e) List the locations of all relative
minima of f.
(6) Use the limit
definition of the derivative to find the derivative of 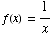 .
.
(7) Find all values of x
for which the slope of the tangent line to the graph of y
= cot(x) at x
has slope ![FormBox[RowBox[{-, 4.}], TraditionalForm]](HTMLFiles/ExF01_73.gif)
(8) Consider the equation 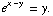
(a) Find 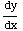 .
.
(b) Find the slope of the tangent line
to the graph of 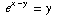 at the point (
at the point (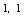 ).
).
(9) Suppose you have 600 feet of fencing
material to enclose two rectangular regions, as illustrated. What dimensions
x and y
would enclose the greatest area?
------------------
| | |
| | |
| | |
-----------------
(10) The height of a conical bucket
is 3 feet and its radius is 1 foot. Water is poured into the bucket at a rate
of 1 cubic foot per minute. How quickly is the depth h
of the water increasing when h =
2?
(11) An object, moving on
a horizontal line, is a distance of 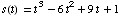 feet
from a point A at time t . (t
is in seconds.)
feet
from a point A at time t . (t
is in seconds.)
(a) At what time(s)
t is the object a distance of 1 foot from the point A?
(b) Find the function giving the object's
velocity at time t.
(c) Find the function giving the object's
acceleration at time t.
(d) At what time(s) t
does the object have a velocity of 9 feet per second?
(e) At what time(s) t
does the object change direction?
(f) When is the object's acceleration
0 feet per second per second?
(g) Find the times at which the object
is speeding up.
(h) When does the object attain its
minimum velocity? (Remember, that velocity could be negative.)