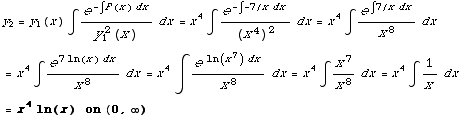Differential Equations Quiz #5 April 1, 2005
Name____________________ R. Hammack Score ______
_________________________________________________________________________________
(1) Verify that the set of functions
First, let's confirm that
y''-y'-12y = 9
Next, let's confirm that
y''-y'-12y = 16
Also, these functions are linearly independent, for
| | | | | ||
Thus, as two linearly independent solutions to a second order homogeneous D.E., these functions form a fundamental set of solutions.
(2) Given that
First, we divide through by
y''-