_________________________________________________________________________________
Differential Equations Quiz
#4 March
18, 2005
Name____________________ R. Hammack Score
______
_________________________________________________________________________________
(1) The function y=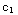 x+
x+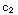 x
ln x is a two-parameter family of solutions of
x
ln x is a two-parameter family of solutions of 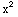 y''-x
y' +y=0.
y''-x
y' +y=0.
(a) Find a member of the
family satisfying y(1)=2 and y'(1)=1.
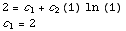
y=2x+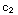 x
ln x
x
ln x
y'=2+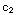 ln x+
ln x+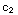
1 = 2+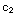 ln (1)+
ln (1)+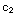 =
2+
=
2+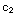
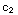 =-1
=-1
The solution to the I.V.P. is y=2x-x
ln x
(b) Is your solution from
part (a) above a unique solution of the initial value problem y(1)=2,
y'(1)=1? Explain.
Yes. The coefficients of y'', y'
and y are 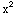 ,
-x and 1, respectively. Each is continuous
and the coefficient
,
-x and 1, respectively. Each is continuous
and the coefficient 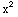 of
y'' is nonzero on an interval containing
1. By theorem 4.1, the solution is unique.
of
y'' is nonzero on an interval containing
1. By theorem 4.1, the solution is unique.
(1) Decide if the following
sets of functios are linearly indepenednt or dependent.
(a) 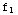 (x)=
(x)=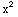 +1,
+1, 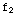 (x)=x+1,
(x)=x+1, 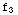 (x)=
(x)=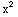 +2+x
+2+x
Notice that 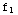 (x)+
(x)+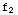 (x)-
(x)-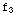 (x)=0
so the functions are linearly dependent.
(x)=0
so the functions are linearly dependent.
(b) 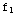 (x)=
(x)=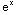 ,
, 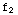 (x)=
(x)=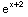
Notice that 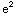
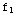 (x)-
(x)-
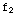 (x)=
(x)=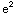
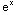 -
-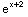
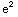 =
=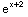 -
-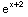 =0
so the functions are linearly dependent.
=0
so the functions are linearly dependent.