Box plots - also known as quantile plots

The box plot is a graphic which display the center portions of the data and some information about the range of the data. There are a number of variations.

The Five Number Summary Box Plot.

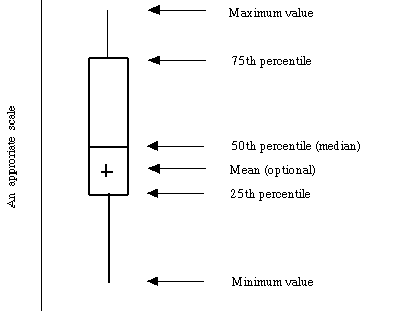
This is a common variant and is drawn by first finding the minimum and maximum values and the 25^th, 50^th, and 75^th percentiles .

Then the box plot (either horizontal or vertical) as drawn as shown below:

Variations on the box-plot Sometimes the whiskers on the box-plot have a different methods of constructions, however, the hinges are are always computed as the 25^th, 50^th, and 75^th percentiles.

• outliers may be identified using an outlier detection rule and are displayed using asterisks or some other character.
• whiskers extend to 10^th and 90^th percentiles;
• whiskers also identify other percentiles; see JMP help on quantile plots

We will make a slight detour here to examine JMP-IN's two types of box-plots and show how to use the help feature to findout what they mean.

Important The actual computation of a box-plot is not that important (that is what computers are used for), but understanding what box-plots show and how to use them is important (what computer can't do!).

Interpreting the box plot

• central box includes the middle 50% of the data

• whiskers show range of data

• symmetry is indicated by box and whiskers and by location of the mean

• it is easy to compare groups by constructing side-by-side box plots as shown below.

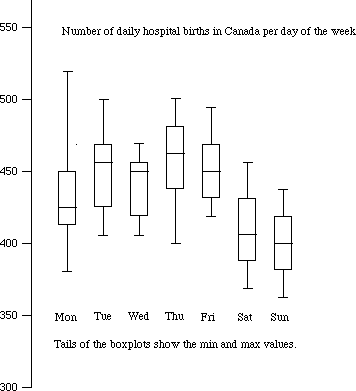
Example of side-by-side box-plot  Here is boxplot of births in a hospital in Canada by day of the week. What patterns do you see? What unusual features are present?