D. C. Mikulecky

Professor of Physiology

School of Medicine

Virginia Commonwealth University

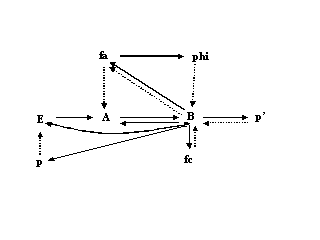
The following relational model is an adaptation of Rosen’s Metabolism-Repair {M,R} model of the organism which incorporates a small amount of additional detail regarding the anabolic/catabolic homeostatic cycle. It is a crude and naïve attempt to add some detail to the defining distinction between organism and machine which Rosen had developed over a 40-50 year period : http://views.vcu.edu/~mikuleck/rosen.htm , namely that the organism is closed to efficient cause and the machine is not.

This diagram also attempts to satisfy a number of other questions which have been asked about Rosen’s {M,R} model pertaining to the organisms relation to its environment. The new diagram is built from the following sets and mappings:

METABOLISM

Transport of materials into and out of the system: The stuff outside is in the set E while its counterparts and other stuff which never leaves the cell are in the set A representing the pool of abstract substrates in the cell. The maps p and p’ are the efficient causes for things entering and leaving the cell

p: E à A

p’: Bà E

Cellular metabolism involves anabolism, the making of larger molecules from subunits, etc. (usually energy consuming events, negative entropy production, etc.)

fa : A à B

And catabolism, the breaking down of larger molecules into smaller units which can either become waste and thereby become eliminated as depicted by the map p’ above, or become building blocks for anabolism:

fc: B à A.

Hence p, p’ fa , fb are functional components and efficient causes for the various material transformations. Further note that our system can only become closed to MATERIAL cause if E, the environment, is allowed to be part of the system. This is important.

REPAIR

Each of the entities p, p’, fa, and fc are subject to catabolic events causing their elimination from the system (notice that this is NOT explicit in the diagram). Therefore they need entailment. The material cause for each of them is the pool of products, B. The efficient cause is the repair map phi. So we have:

Phi : B à p

Phi : B à p ‘

Phi : B à fa

Phi : B à fc

REPLICATION

Phi itself needs to be made if it also is subject to catabolic destruction. The inverse map from B to phi, {b} mappings developed by Rosen does this nicely if we simply assume that this group of mapping are all anabolic in nature and therefore only involve fa (this assumption is not necessary, but simplifies matters a bit):

{b} : fa à phi

For the math buffs, this is a bit sloppy, but I think it should be clear that what has been glossed over is pretty obvious as you rewrite the mappings in the f à H[A,B] format.

To me, this is an instructive exercise because it shows the difference between merely manipulationg diagrams OR category theory expressions without semantic context and dealing with the semantics in a straightforward manner.

THE DIAGRAM:

So now we have a more complicated diagram. Does it conform to any we have seen before other than Rosen’s?