ABSTRACT: Cubism was a significant "paradigm shift" in painting just after the turn of the century. It has been associated with changes in science which were happening in parallel with its advent. However, the thesis of this work is that the nature of the paradigm shift, of which cubism was the transitional representation, had a new notion of space and time as its "trademark", but, in fact was a deeper transition than even that. In order to demonstrate this, certain parallels between art and science are developed. In particular, the way the human mind deals with both art and science are shown to have certain similar characteristics, which are best formulated in terms of the modeling relationship. The modeling relationship concept is used to emphasize the interactive nature between human cognition and the subject matter of both art and science. Having established this, it is then shown that cubism introduced an artistic equivalent of complexity into the modeling relation underlying painting. The term complexity is defined with some care and its applicability to art as well as science is established. Finally, the fact that cubism was actually the introduction of complexity into painting at the turn of the century, is shown to make this art form a forerunner of some of our most recent breakthroughs in scientific thinking. In order to do this, it is shown that the difference between non- computable formalisms and computable formalisms in scientific complexity has a strong parallel in the difference between pictorial painting and representational painting. It is this character of cubism rather than the mere change in space-time perception which it entails which is its major contribution to our current intellectual situation. The use of computers in art and, in particular, the use of fractal geometry in art, will be shown as a retrogressive intellectual step when viewed in this context. The computability of this form of art makes it "simple" and "mechanistic" when compared to cubism as a complex art form.
INTRODUCTION The painting style called "cubism" evolved over a period of time and resulted in a new way of pictorializing subject matter [Gerhardus,1979]. Without getting into too much detail, it is worth tracing the nature of this change. Most authors seem to agree that in the work of Cezanne the seeds of the cubist idea were already being manifested [Gray, 1953]. This idea is best illustrated using the idea of passage as an example. What Cezanne did by this continuation of a line through a painting, involving it in background and foreground, was an essential component of the cubism which would follow. The effect on human perception was both subtle and profound. The continuity of a line changed perception and broke down the identity of three dimensional objects to be, in a sense, more compatible with the two dimensional surface on which the painting exists. This effect, in turn, freed the mind to utilize parts of the painting, space, in the generation of new, exciting patterns which would not have been possible had the usual "rules" for dealing with lines for perspective and shadow and light for perception of three dimensions been followed. (The discarding of "natural" representations of light and shadow being an integral part of the final manifestations of cubism). My thesis is that this breakthrough is strongly parallel in its nature to one which is being manifest in science in the last decade or so, well after it was already a piece of history in painting. In order to develop this idea, it will be necessary to discuss the issue of complexity as it is being discussed in science. The parallel I wish to make is between the new perception of relationships on the canvas in cubism, and the new relationship of whole to parts in our perception of the natural world through science. As a tool for making the perceptive process concrete and analyzable, the modeling relation must become the central idea. Through this representation of how we operate in our attempts to "objectify" the world we perceive, we will be able to see what complexity entails and examine its nature in detail. Though I will be discussing these ideas from the viewpoint of the way they were developed for science and its epistemology, it should become clear that the ideas are more general and are also useful in the discussion of the perception of art.

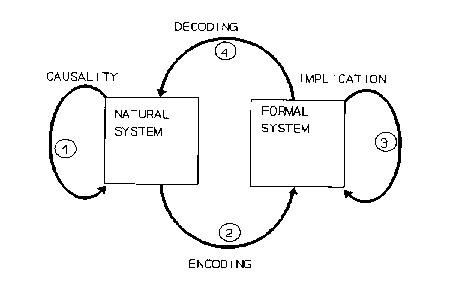
Fig. 1: The Modeling Relation
DEFINITIONS The Modeling Relation: The figure shows two systems, a so called "natural system" and a "formal system" related by a set of arrows depicting processes [Rosen, 1978,1985,1991]. The assumption is that when we are "correctly" perceiving our world, we are carrying out a special set of processes which this diagram represents. The natural system is something in our surrounds which we wish to "understand" (as well as control and make predictions about, if these are distinguishable from "mere" understanding). In particular, arrow 1 depicts causality in the natural world. Embedded in this representation is our belief that the world has some sort of order associated with it; it is not a hodge-podge of seemingly random happenings. On the right is some creation of our mind or something our mind "borrows" in order to try to deal with observations or experiences we have with our surrounds. The arrow 3 is called "implication" and is some way we manipulate the formal system to try to mimic causal events. The arrow 2, is some way we have devised to encode the natural system or, more likely, select aspects of it, in terms of the formal system. Finally, the arrow 3 is a way we have devised to decode the result of the implication event in the formal system to see if it represents the causal event's result in the natural system. Clearly, this is a delicate process and has many potential points of failure. When we are fortunate to have avoided these failures, we actually have succeeded in having the following relationship be true:
1 = 2 + 3 + 4.
When this is true, we say that the diagram commutes and that we have produced a model of our world. Complexity: In science, the modeling relation which has been dominant for centuries came to us some time ago through the work and thinking of Descartes, as was formalized by Sir Isaac Newton. We will refer to this particular way of perceiving the world as the "Newtonian Paradigm" [Rosen, 1991] and the closely allied Cartesian epistemology as "reductionism" [Peacocke, 1985]. In short, most of the advances of modern science are based on this approach. In science and most of human activity reductionism has become ontological. That is, wholes are seen as merely the sum of their parts and Descarte's machine metaphor and dualism (mind/body) are the dominant ideas we encounter. The most recent manifestation of this way of modeling the natural world is "molecular biology" which, in fact, can be said to be an oxymoron. If biology is the study of life, it surely requires the retention of higher levels of organization than the molecular! But this one method of viewing our world has become dominant and , in fact, is the basis for a form of snobbery which criticizes areas such as sociology and psychology for being "soft" sciences which are not readily able to "beat" their subject matter into a form which conforms to the Newtonian/Cartesian mold [Rosen, 1991]. The alternative to this reductionist/mechanistic approach, which has been the basic subject matter of traditional physics, is often termed "complexity" or "complex systems". The implication, then, is that physics, at least traditional physics, is concerned with "simple systems" or "mechanisms". The new fields of chaos (part of non-linear dynamics) and fractal geometry are among the most well known manifestations of the new science of complexity. However, the real issues in complexity go deeper than these manifestations. Ironically fractal geometry is antithetical to complexity in art. Given the notion of perception described by the modeling relation, and given the historical roots of science since Descartes, there is necessarily a subjective component to this classification. However, from an epistemological point of view, this is an inevitable component of human intellectual endeavor and we simply acknowledge this and use it to help us understand the categorization. Let us then proceed to understand what distinguishes simple from complex systems in science and then use this understanding to see that cubism is a parallel and earlier development in painting. We will use the following working definition of complexity: A system is complex to the extent that we have more than one distinct way of interacting with it. This will necessitate more than one model. Remember that a commuting modeling relation is a single model. Distinct, in this sense means that one model is not derivable from another. This usually means that the formal systems on the right hand side of the modeling relation are distinct. it can also involve the encoding and decoding. The more general statement about complex systems is that there is no largest model, from which all others might be derived. Thus, to the extent that a single description suffices to describe our interactions with a system, we call it simple. If this fails to be true, we call it complex.
COMPLEXITY IN ART, LITERATURE, AND SCIENCE
The role of the observer
The subjective component to this categorization must now be dealt with. In a very real sense all natural systems are complex. We saw them as simple for hundreds of years only because we had no tools to interact with them in more than one way. This means both experimental tools and theoretical tools. The revolution in progress in science is so dependent on the fact that the new tools now exist that our necessary introduction of subjectivity is really nothing more than an acknowledgement of an epistemological reality. The more important question for the purpose of this essay is whether or not the same is true of cubism relative to the painting that preceded it. Clearly, this is the thesis we wish to develop. In order to do that, we will need to develop some clearer manifestation of complexity in science and then show that there are strong parallels between these manifestations and the new features cubism brought to painting. It might be evident from these definitions that what we intend to argue is that cubism introduced complexity into painting by increasing the number of distinct ways we may interact with a painting. This point is, hopefully, easy enough to accept on the basis of traditional analyses of cubism. However, these interpretations focus on the use of space and other ideas which are certainly pertinent in the analysis, but also somewhat misleading (for example, Shlain [Shlain, 1991] puts cubism into the reductionist framework of physics, seeing it as merely a reduction or fragmentation of an object into planes.) It is really the subjective aspects of those features which make the essential difference. Let us proceed to examine this idea through analogy. Complexity in science as a model for complexity in painting Our tool for this comparison will be the modeling relation. We will put the cubist paintings as a category in the position of the natural system and the formal system will be complex systems science. It is our job to develop an encoding and decoding such that the diagram commutes. To facilitate the evaluation of the commutivity of this modeling relation, we will also use a third system to relate to the other two through two other encoding and decodings. This third system is poetry and literature. The reason for this is that we wish to dwell on one aspect of complex systems which is paramount in making it impossible for them to have a largest model. This aspect is the presence of some impredicativity in the form of a non-computable component. Impredicativity is the property of self reference. It implies a context dependence typical of the semantic rather than the syntactic aspects of systems. It therefore rules out the possibility of the computation of the feature. In literature we speak of the difference between syntax and semantics. In other words, we are speaking of something that necessitates our being both subject and object in the process. Syntax is a concept which carries over from language to computer language and the limits of computers. To say it as briefly as possible, it is a way of encoding things so they can be processed by a universal Turing machine (UTM) [Fischler and Firschein, 1987]. Syntactical machines, such as the UTM, involve an "alphabet" of symbols and rules or algorithms for processing them to obtain the theorems of the formalism. Turing conceived the UTM solely as a thought experiment for discussing this process. It has never actually been realized. Our modern computers are special cases of this UTM. Thus, the hypothetical UTM represents the best we can expect from computers. Things computable with syntactical machines are simple. So complex things involve semantics. Here's where literature can be of a great help to us. In Robert Frost's poem "Stopping by the woods on a Snowy Evening" the last stanza reads:
The woods are lovely, dark, and deep,
But I have promises to keep,
And miles to go before I sleep,
And miles to go before I sleep.
This example came up in a recent symposium on the machine metaphor in science and the nature of complexity [Henry, 1995]. Henry emphasizes the formal identity in syntax and rules of grammar in the last two lines. He stresses that they are not equivalent semantically and are highly context dependent. A related example would be in the writings of Gertrude Stein who uses a similar device in writing about Picasso [Burns, 1970]:
One whom some were certainly following was one who was completely charming.
One whom some were certainly following was one who was completely charming.
One whom some were following was one who was completely charming.
One whom some were following was one who was certainly completely charming.
It is significant that a number of authors discuss Stein's writing with respect to its
analogy with cubist art [Fry, 1966; Burns, 1970; Dupee, 1990; Gray, 1953; Benstock, 1986].
This topic and the issue of semantic vs syntactic content in linguistics is a topic of
great importance [Pinker, 1994]. It is also interesting to note the way Picasso's poet
friend organized words into patterns [Apollinaire, 1913]. The distinction between syntax
and semantics in language parallels closely the distinction between computable and
non-computable aspects of natural systems in science. As a concrete example, the Bénard
systems will be examined. The Bénard phenomenon The Bénard phenomenon is striking
because it arises in a layer of water with a thermal gradient across it. Other fluids will
work as well, so it can not even be explained in terms of the molecular properties of the
liquid. For the last 15-20 years I have used a device produced by Paul Matisse, Henri
Matisse's son to demonstrate the phenomenon to my classes. It was purchased from the
National Gallery of Art! This device, called a Kalirascope, was designed to produce
whirling patterns in a rectangular container filled with a viscous fluid dyed blue and
having a substance mixed with it which gives silvery blue color if the fluid flows. It
came with a spinner so it could sit on a table and be spun. The flow patterns in the
turbulent fluid would produce amazing patterns. To demonstrate the Bénard phenomenon it
is merely necessary to remove the spinner attachment and pour cold water on the surface of
the container. It is classically demonstrated by placing a petri dish of water on a hot
plate. The setup is shown in figure 2. 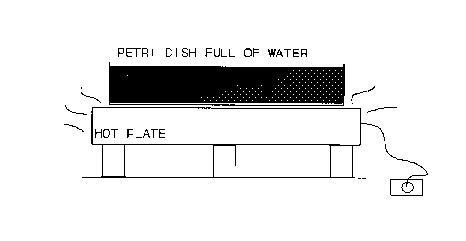
Fig. 2: The Bénard System
Heating the water from below creates a potentially unstable situation since the cooler
water at the top is more dense and tends to "fall" to the bottom. If the
temperature gradient is not too large, the instability is avoided and normal thermal
diffusion will occur. At some critical gradient, an unstable condition is reached and the
water "organizes" itself into hexagonal cells in which convection occurs.Figure
3 is a drawing of the result of such organization as viewed from above. 
Fig. 3:The hexagonal cells viewed from above
Figure 4 depicts the pattern of flow in the system once the convection cells are established.
Fig. 4: The flow pattern
The flow patterns and heat conduction process are simple a spontaneous response to the imposed temperature gradient. They are readily described by classical physics. [Chandreshaher, 1961]. What is novel and , in a sense, disturbing to classical physics is the self-organization of the fluid into hexagonal convection cells. There is no way of explaining this in terms of the reductionist/mechanistic paradigm! Moreover, the system can be simulated on a computer before and after the transition to the hexagonal cells, but the transition itself is beyond any computation we know. It is like the process, also poorly understood, that leads to the assigning of different meaning to the two last lines of frost's poem, the effect of repetition in Stein's writing, or the use of patterns of words in Apollinaire's poetry. What is the parallel to these examples in cubist painting? The beginnings are in Cezanne's paintings and his use of passage, grid like structure and color and lighting to produce meaning that transcends the usual representational painting techniques. In the use of passage in the painting of Zola's house (Zola's House at Medan, 1880) the lines which are common to the edge of a house in the background and trees in the foreground are continued as part of a horizontal/vertical grid which creates a meaningful manipulation of space on the canvas which has no necessary reality in the scene which has been painted. The space begins to take on a meaning which can not be given any sort of algorithmic formulation. The effect is a form of non-computability in the very same sense that we recognize this property in the complexity of natural systems such as the Bénard system or language as in the cases mentioned. Later, in analytical cubism in particular, this phenomenon is exploited to a greater and greater extent producing a few more effects which also can be associated with complexity. Lets us examine these more carefully.
Cubist art as a special metasystem
One of the most interesting aspects of new research in complexity is a renewed interest in consciousness and the mind/brain problem [Searle, 1955]. This is an area with several distinct facets. One of them is the issue of "Hard" and "Soft" Artificial Intelligence (HAI and SAI). HAI is basically the position that computers are brains and vice versa. SAI is the idea that even though the brain is very different from computers, its mode of operation can be simulated on a computer. Searle discusses this issue with some lucidity in his recent article, and it has a relevance to this discussion. The possibility of HAI is refuted by so many authors that we can assume that it is not an issue for the purposes of this discussion. The issue which is of importance here is the question of computability which is at the center of the SAI issue. The argument can be summarized as follows: Due to a number of factors, too technical to delve into here ( the halting problem, Gödel's incompleteness theorem and others [Fischler and Firschein, 1987], the issue of computing the necessary algorithms on a Turing type (our modern digital computer is an example) computer as well as the very existence of such algorithms is out of the question. However, there may be flaws in the argument leading to this conclusion if we allow for other types of computation. I find this position rather shallow, at best. It is as if to say that no proof in our system of thought is final, because we may someday come up with something new! So be it. In the meantime, it would seem safe and reasonable to proceed on the assumption that what we know is what we know and that, quite simply stated in this case, is the fact that minds and other complex systems do things that are not computable and therefore neither hard or soft AI are tenable. This conclusion is central to dismissing the most obvious objection to my placing cubist art in the category of complex systems along with number theory, language, and modern science's view of the natural world. It is quite impossible to show directly that cubist painting is not computable. It is, however, possible to make as strong a case for this as has been made in these other, more well argued about areas. If, and this seems extremely doubtful, in the future, a new wrinkle will appear which causes the argument to fall, they will all fall together. We should be able to agree to cross that bridge if it ever becomes necessary. More important for the argument being made here, is the observation Searle makes as an additional point to support his own preference to accept the SAI position while rejecting the HAI position emphatically. He is willing to suppose that some, if not all the processes going on in the brain are simulable. This is, no doubt, based on the almost miraculous progress being made in the field of artificial neural networks. These devices mimic the massively parallel structure of the human brain and seem to work in the same way [Rosen, 1994]. They are based on Hebb's theory of what we have come to call associative memory. The striking thing about these networks is their ability to reconstruct an image, for example, from incomplete fragments. We will come back to this very important point. In a nutshell, Hebb's theory places this form of memory in the strength of connections between neurons, the synapses [Altman, 1989]. In short, use strengthens the connections between neurons and disuse weakens them. Artificial neural networks capitalize on the ease with which this idea cam be implemented in an artificial system. Ironically, this highly effective leap beyond the Turing type computer is most frequently implemented by simulating it on a Turing type computer! And here of course is the problem. This activity is certainly simulable up to a point. It is certainly true that to the extent that an image can be encoded into a string of ones and zeros, the computer simulation will often successfully reconstruct that string from incomplete or "noisy" versions. To the extent that the encoded image can be represented by patterns of pixels on a computer screen, for example, the image can be made visual. But this is the point! The artificial neural network can only produce the string of ones and zeros. Something more must provide the interpretation. In a computer simulation, this is an extra piece of software which may place an image on the computer screen. It does not originate with the artificial neural network and hence is part of a metasystem. It has been argued that the same is true in art. A painting is "merely" a set of marks and colors on a surface. It takes a human being to associate these marks and colors into a semantic reality (see the quote of Picasso below, for example). The same is true in literature. But this is precisely the point! When an artificial neural network reconstructs a letter of the alphabet from a fuzzy version, it does so because it was previously trained to recognize that letter's binary code as a member of the set of binary codes for a set of letters. The realization of these codes as letters of the alphabet requires a significant extra step. The simulation can deal with this nicely because it successfully simulates a computable process. When Picasso and Braque produce images which are incomplete versions of a violin or person, we also reconstruct these in our minds, but not by computation. This is not a simulation but a higher level, complex event which could not be turned into an algorithm. Very possibly it involves a mechanistic, computable component as does the activity in the artificial neural network, but now, if we are at all still dealing with a metasystem, it is totally contained within the brain. This is the distinction we have been making between brains and computers for some time and it is interesting to see that Searle recently discovered it on his own and found it very compelling! In summary then, the subject nature of complexity is apparent here also. The interaction between the art object and the viewer is a metasystem. The art object is complex in that through this interaction, a component of the brain, which itself is a self-contained metasystem, is activated. This activity is capable of seeing the complex nature of the object, rather than just the obvious lines, marks, and colors on the surface. This event strikes at the very nature of consciousness and perception. It has lesser manifestations in other forms of art, but these are basically algorithmic in nature. This is the real meaning of the manipulation of space and other facets of cubism such as the use of "signs and symbols" to activate associative memory. No artificial neural network could reproduce the image of a guitar from a cubist painting. The painting is more than a "noisy" image of a guitar. In fact, it is very possible that some of the meaning of a cubist painting is processed at a sub-conscious level. We do not expect to ever have algorithms for this. The ultimate non-computable aspect of cubism: self-reference The ultimate form of non-computability is self-reference. This idea is at the heart of of what distinguishes simple mechanisms from complex systems in science. It also is the central component to G"del's incompleteness theorem. One way of illustrating the idea is to imagine a system of logic wherein we have the statement: "This statement is not verifiable within this system." Clearly everything breaks down at this point. If the statement is true, it proves the system is not complete. That is, it doesn't contain sufficient power within itself to verify all is theorems. On the other hand, if the statement is false, then the system is not consistent, i. e. it allows for false statements or contradictions. What Gödel was able to show is that no system can be simultaneously complete and consistent [Fischler and Firschein, 1987]. Hence the inevitability of the need for metasystems as was exemplified in the previous section. There is a self-referentiality or impredicativity in the examples of language we have examined above. The cubism of Picasso and Braque during the period before the First World War is replete with a hierarchy of self reference. To my knowledge, no other period in the history of painting is like this. Let us look at but a few of the many examples. In a single painting Scallop shells (1912) the letters "JOU" have at least a triple meaning all of which involve a self-reference. The letters can be interpreted as standing for part of the word "jour" which is French for "day". They also might refer to the practice of using newspapers in the paintings which might date the painting (giving the day). These newspapers are being symbolized by JOU as a part of "journal" or newspaper in French. Ah, but the use of only part of a word to invoke an idea in the mind of the viewer is exactly the associative memory process we discussed in the previous section and is playing along with the broader use of this practice. Finally, the French word "jouet", "to play", is also suggested. These words or fragments of words are usually stenciled on the painting and also serve to emphasize the fact that the painting is merely a two dimensional surface. This is indeed also a part of an ongoing "game" between the two artists. Other examples of repeated references to each other's paintings are to follow as their dialog progresses. Wood grain, bits of rope, table edge decorations and many other ploys pepper these paintings in the form of an ongoing conversation between the two artists. Picasso carries this a step further in musical instrument (1912) by painting the pasted paper and wallpaper! In this manner, the two painters brought to their art a component which is the essence of complexity and the antithesis of computability. A more subtle form of self reference shows up most often in Picasso's paintings. There is often evidence for his letting a painting evolve as it is being produced so that the process and the product become self-referentially entwined. Often this goes to the extreme of his actually painting over the work as in the Portrait of Gertrude Stein (1906) and Demoiselles d'Avignon (1907). It is best said by Picasso himself (An interview by Christian Zervos) [Cooke, 1972]:
"I do a picture-then I destroy it. In the end, though, nothing is lost: the red I took from one place turns up somewhere else".
"...Basically a picture doesn't change; the first 'vision' remains almost intact, in spite of appearances..."
"A picture is not thought out and settled beforehand. While it is being done it changes as one's thoughts change. And when it is finished, it still goes on changing, according to the state of mind of whoever is looking at it. A picture lives a life like a living creature, undergoing changes imposed on us by our life from day to day. This is natural enough, as the picture lives only through the man who is looking at it..."
"When you begin a picture, you often make some marvelous incidental effects. You must be on your guard against these. Destroy them, and do the passage over several times. Each time he destroys an incidental effect, the artist does not really suppress it, but rather transforms it, condenses it, and makes it more substantial. What comes out in the end is the result of discarded finds, otherwise, you become your own connoisseur. I sell myself nothing..."
The comparison of the picture with a living creature was Picasso's own realization that he was dealing with the ultimate form of complexity, the analog of organic life!
Computer generated art and fractal art
This brings us to an interesting paradox. One of the recent "fads" in computer science and related areas is to generate elaborate patterns using mathematical algorithms. This is computability in the most blatant sense. The fractal patterns, in particular, are often very intricate and colorful. They can be programmed to reproduce scenes like landscapes for example, and can be made deceivingly "realistic". From the viewpoint developed here, these are simple systems and do not merit comparison with complex forms of art. They are again an example of mimicry [Rosen, 1994]. What the metasystem we call art is most notable for is its generation of complexity. Thus, I will predict that once the fascination with computer generated art forms has had its "fifteen minutes of fame" it will result in an even greater effort to generate new, non-computable, complex forms.
Summary and conclusions
Cubism introduced complexity into painting by introducing the analog of non-computable elements found in literature and science. It created a model, which we have analyzed here using the modeling relation, which is dynamic and more process-like than the result of a series of rules or algorithms. By so doing, it freed twentieth century art to escape the constraints of rules, formulas and computable methods. At present, we are in a position to observe a real paradox. As the ideas which are manifest in cubism are taking over science and other fields more than fifty years later, the influence of the mechanistic/reductionist thinking that spilled over from science to permeate all of human activity is also presenting a challenge to art in the form of the antithesis to cubist complexity, namely computer generated art. As the revolution in thought called "complex systems" moves onwards, there are counter-revolutions which will spring up from time to time. In biology, this is typified by certain proponents of molecular biology which is peaking now only because the technology for its implementation was so long in coming. Eventually, the legitimate role of this special version of physics and chemistry will be put into perspective. In industry, a battle is being fought over complex vs computable forms of organizing operations. Robotics is also a common way of trying to treat all of the manufacturing process as a mechanism rather than a complex system. Modern economic theory is replete with reductionist ideas. The revolution touches each of these. Economic theory of a very different kind which grows out of the work of Brian Arthur makes holistic sense and speaks towards a new way of looking at adaptive, evolving systems [Waldrop, 1993]. Manufacturing process can be approached from a complex systems perspective [Casti, 1994]. We seem to be going through an instability and period of transition which is very much of the same nature as the industrial revolution [Capra, 1982]. As during that period, there is no aspect of human society which is immune. It seems just possible that the first signs of this upheaval came just after the turn of the last century in the form of quantum physics, cubism, and related epistemological transitions.
Acknowledgement: I wish to thank Professor Howard Rizzati of VCU's Art History Department for many of the insights expressed in this paper.
REFERENCES:
Apollinaire, G. (1962) The Cubist Painters: Aesthetic Meditations 1913, (translated from the French by Lionel Abel) George Wittenborn, Inc., NY.
Altman, W. F. (1989) Apprentices of wonder: Inside the neural network revolution, Bantam Books, NY
Benstock, S. (1986) Women of the Left Bank:Paris, 1900-1940, Univ. Texas Press, Austin.
Burns, E. (ed.) (1970) Gertrude Stein on Picasso, Liveright, N. Y.
Capra, F. (1982) The Turning Point: Science, Society, and the Rising Culture, Bantam Books,
Casti, J. L. (1994) Complexification, Harper Perennial, NY.
Chandrasekhar, S. (1961) Hydrodynamic and hydromagnetic stability, Oxford University Press, London, pp 9 - 219.
Cooke, H. L. (1967) Painting Techniques of the Masters, (revised ed. 1972), Watson- Guptill Pubs., NY.
Dupee, F.W. (1990) Selected Writings of Gertrude Stein, Vintage Books, NY. Fischler, M. A. and O. Firschein (1987) Intelligence: The eye, the brain, and the computer, Addison-Wesley Pub. Co., Reading, MA.
Fry, E.F. (1966) Cubism, Oxford Univ. Press, NY.
Gerhardus, M. and Gerhardus, D. (1979) Cubism and Futurism, Phaidon, Oxford.
Gray, C. (1953) Cubist Aesthetic Theories, The Johns Hopkins Press, Baltimore.
Henry, C. (1995) Universal Grammar, in Self-reference in cognitive systems and biological systems, (L. Rocha,ed) CC-AI 12:45-62.
Pinker, S. (1994) The Language Instinct: How the mind Creates Language, Wm. morrow and Co., NY.
Peacocke, A.R. (1985) Reductionism in academic disciplines SRHE & NFER-Nelson, Surrey.
Rosen, R. (1978) Fundamentals of Measurement, North-Holland, Amsterdam.
Rosen,R. (1985) Anticipatory systems, Pergamon, London.
Rosen, R. (1991) Life Itself, Columbia Univ. Press, NY.
Rosen, R. (1994) On Psychomimesis, J. thoer. Biol. 171:87-92.
Saussierre, Ferdinand de (1959- English Translation by W. Baskin) Course in General Linguistics, (C. Bally and W. Baskin, eds.), McGraw-Hill, NY.
Searle, J. (1995) The astonishing hypothesis: The scientific search for the soul, NY Review of Books, Vol. XLII, No. 17: 60-66.
Shlain, L. (1991) Art & Physics: Parallel Visions in Space, Time & Light, Wm. Morrow and Co.,NY.
Waldrop, M. M. (1992) Complexity: The Emerging Science at the Edge of Order and Chaos, Touchstone, N. Y.