Example 3: Plane-curve plotting (multiple curves, explicit or implicit)

Objective: To show by examples how to plot plane curves in a variety of ways.

Example 3A. (Explicit function plotting) Graph the function of one variable

y = f(x) = 2[e^(-x/2)]sin(ax)

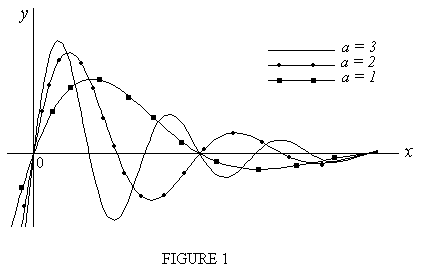
and use the scrollbar to examine the shape of the function as the parameter a ranges betweem 1 and 3. Plot the graphs for the three values a = 1,2,3 in the same coordinate system. Decide on good ranges of values for x,y.

Click here for the .dpg file containing the needed commands. When this file opens on your screen, click the "Scrollbar" on the top menu (or press [alt][r]) and then click "A variable" for the parameter a (the two "a"s need not be the same; we might have sin(kx) for example, but enter "a" in the graph3d(...) command instead of "k"). The starting value of a in the scrollbar is 3, so lower it towards 1 and observe what happens to the curve. Note the following:

• You may change the range of a by clicking "Edit" (or pressing [alt][e]) and then changing the values for one or both of "a.maximum" or "a.minimum".

• To enter axes, add the two equations x = 0 (the y-axis) and y = 0 (the x-axis) in the graph3(...) command. Refer to the .dpg file for the correct syntax.

• The range of values for x and y as seen in the "Edit" dialog box (under commands "graph3d.minimumx", etc.) seem to give a good sense of the graph and its oscillatory and decaying character. The range for "z" is chosen so that the third dimension is too thin to be seen (this is a two dimensional problem).

Figure 1 below shows the graphs for a = 1,2,3 in the same coordinate system. See the "software" page for hints on how to create multiple plots using MS Paint.

 

Example 3B. (Implicit equation plotting) Plot and explore the graph of the following equation in two variables:

3(x + y) - x^3 - y^3 = a, (a = 2)

Click here for the .dpg file containing the needed commands. Note that it is not easy to solve this equation explicitly either in terms of x or y. So we cannot easily graph this equation in the same way as in Example 3A above. However, DPGraph can produce an implicit plot of this equation directly (see the last line of commands). A graph appears in Figure 1 for a = 2:

Note the following:

• By enlarging ranges for x,y it is a good idea to make sure that there are no other bounded pieces.
• Do you know how to show that the bounded piece of the curve touches the two axes at 1 each, as indicated in the graph? The unbounded piece crosses each of the two coordinate axes at a point also; what are these intersection points?

Next, use the scrollbar to reduce the value of a down to zero and then into negative values. Observe the changes that take place. You may plot several snapshots of this in one coordinate system as in Figure 1 of the previous example. A sample multiple-plot diagram is shown in Figure 2 below for a = 2, 1, 0.5, 0.